A horizontal stick of mass m has its right end attached to a pivot on a wall, while its left end rests on the top of a cylinder of mass m which in turn rests on an incline plane inclined at an angle θ. The stick remains horizontal. The coefficient of friction between the cylinder and both the plane and the stick is μ. Find the minimum value of μ as function of θ for which the system stays in equilibrium.
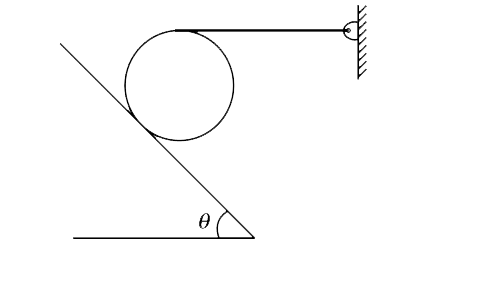
The correct Answer is:3sinθ1+cosθ
Similar Questions
A solid cylinder of mass 8 kg and radius 50 cm is rolling down a plane inclined at an angle of 30∘ with the horizontal. The minimum value of coefficient of friction so that cylinder does not slip while rolling down the plane.
View SolutionA horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
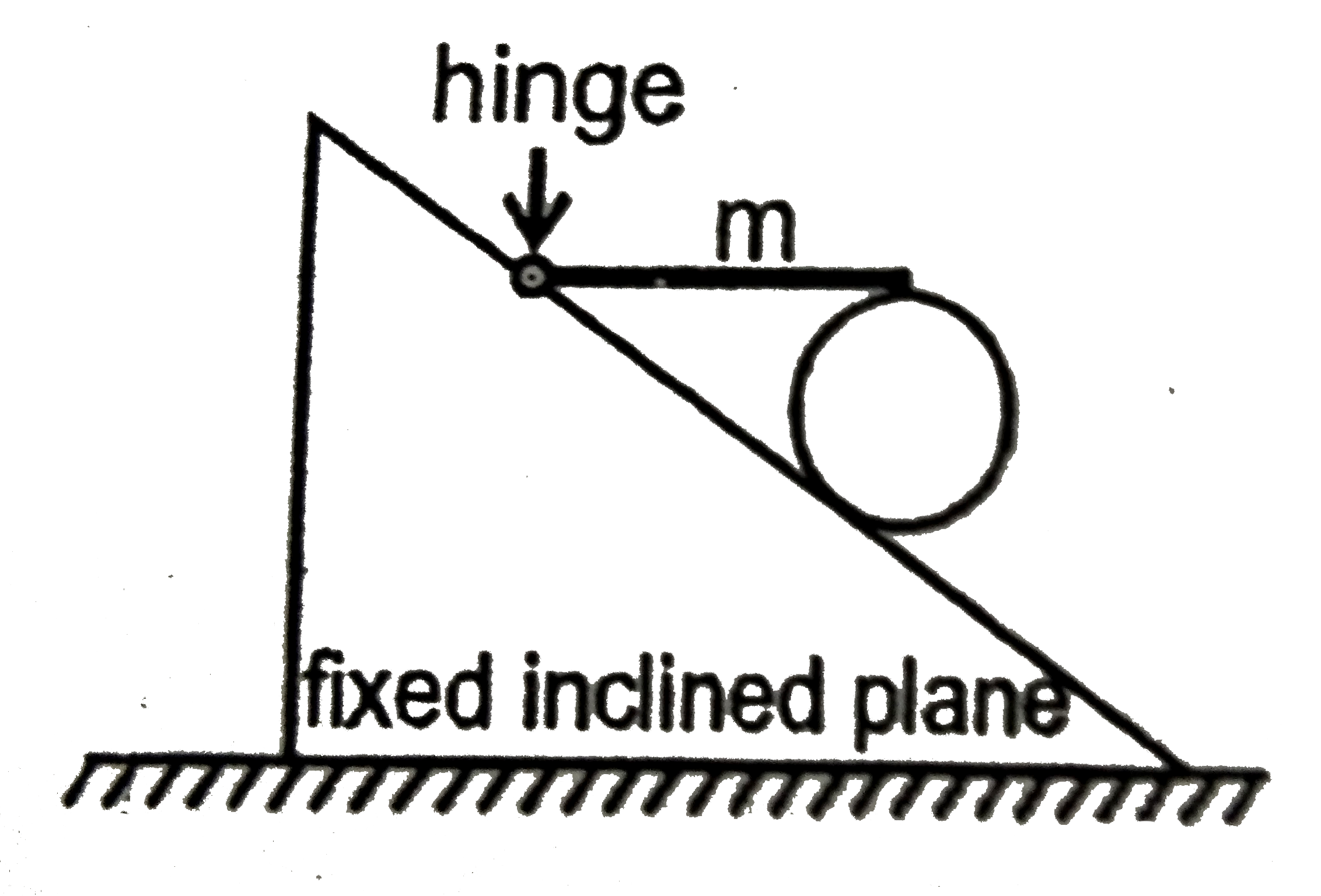
The magnitude of normal reaction exerted by the inclinded plane on the cylinder is :
View Solution
Knowledge Check
A solid cylinder of mass m rolls without slipping down an inclined plane making an angle θ with the horizontal. The frictional force between the cylinder and the incline is
AmgsinθBmgsinθ3CmgcosθD2mgsinθ3A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1DμmgθA horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.

The ratio of magnitude of frictional force on the cylinder due to the rod and the magnitude of frictional force on the cylinder due to the inclined plane is :A1:1B2:√3C2:1D√2:1
A horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
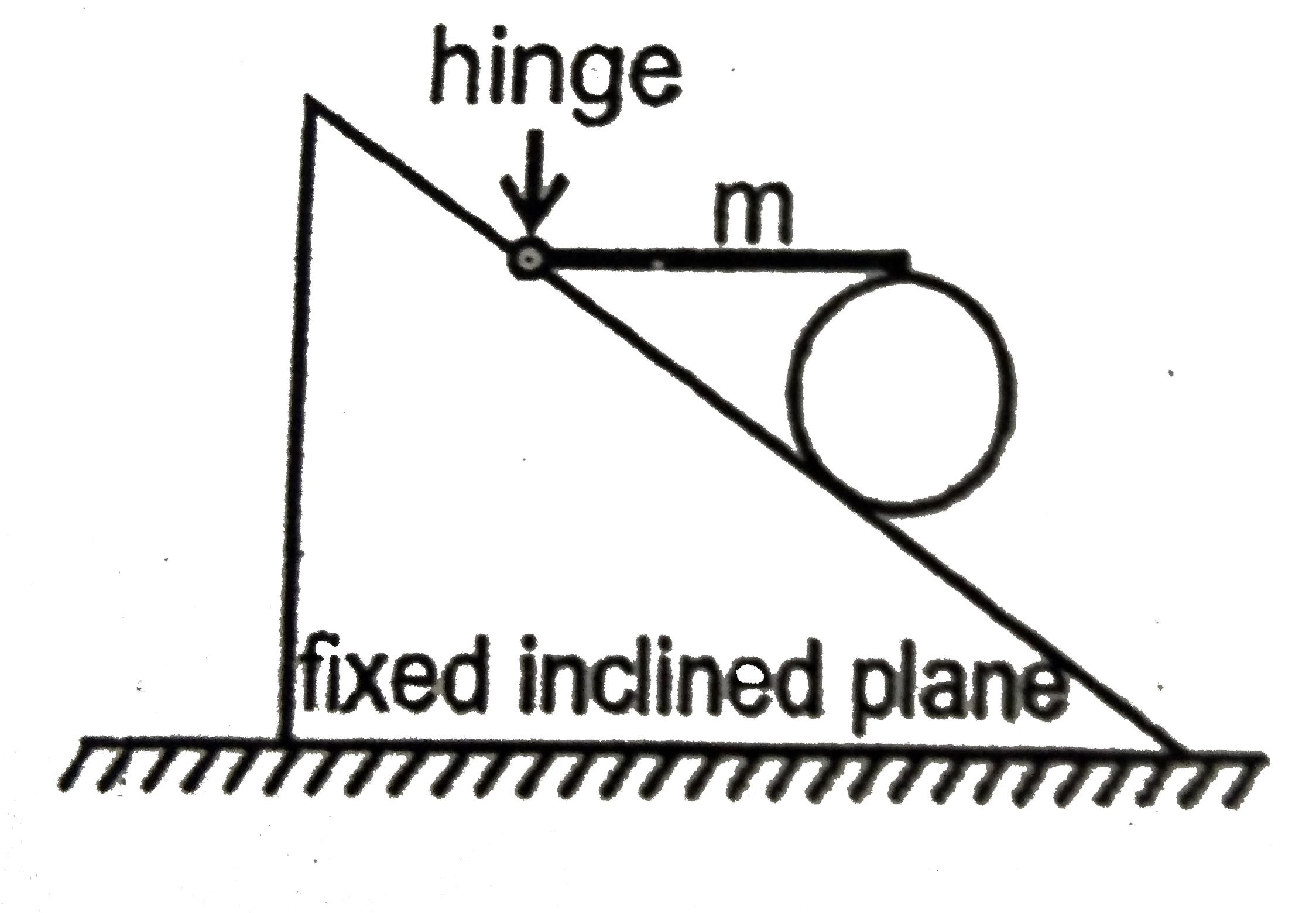
The magnitude of normal reaction exerted by the rod on the cylinder is
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View SolutionA solid cylinder of mass M and radius R rolls from rest down a plane inclined at an angle θ to the horizontal. The velocity of the centre of mass of the cylinder after it has rolled down a distance d is :
View SolutionA solid cylinder is rolling down on an inclined plane of angle θ. The minimum value of the coefficient of friction between the plane and the cylinder to allow pure rolling
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View Solution

