In the figure shown, the light thread is tightly wrapped on the cylinder and masses of plank and cylinder are same each equal to m. An external agent begins to pull the plank to the right with a constant force F. The friction between the plank and the cylinder is large enough to prevent slipping. Assume that the length of the plank is quite large and the cylinder does not fall off it for the time duration concerned.
(a) Find the acceleration of the cylinder. (Hint : don’t write any equations)
(b) Find the kinetic energy of the system after time t.
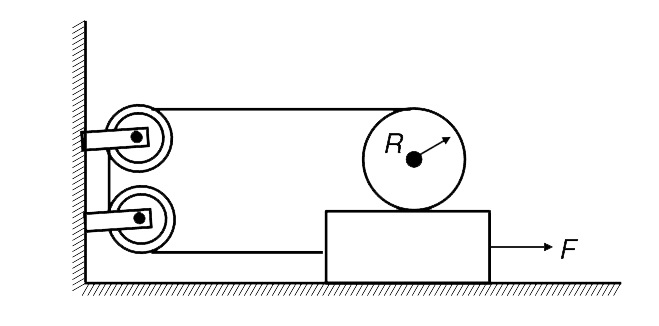
The correct Answer is:(a) Zero
(b) F2t23m
Step by step video, text & image solution for In the figure shown, the light thread is tightly wrapped on the cylinder and masses of plank and cylinder are same each equal to m. An external agent begins to pull the plank to the right with a constant force F. The friction between the plank and the cylinder is large enough to prevent slipping. Assume that the length of the plank is quite large and the cylinder does not fall off it for the time duration concerned. (a) Find the acceleration of the cylinder. (Hint : don’t write any equations) (b) Find the kinetic energy of the system after time t. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A plank of mass M is placed on a rough horizontal force F is applied on it A man of mass m rens on the plank find the acceleration of the man so that the plank does not move on the surface . The coefficent of friction between the plank and the surface is μ Assume that the man does not slip on the plank

View SolutionThe diagram shows a rough plank resting on a cylinder with one and of the plank on rough ground. Negtect friction between plank and cylinder. Draw digrams to show
(a) the force acting on the plank,
(b)the force acting on the cylinder.

View Solution
Knowledge Check
In the figure shown, the plank is being pulled to the right with a constant speed v. If the cylinder does not slip then:
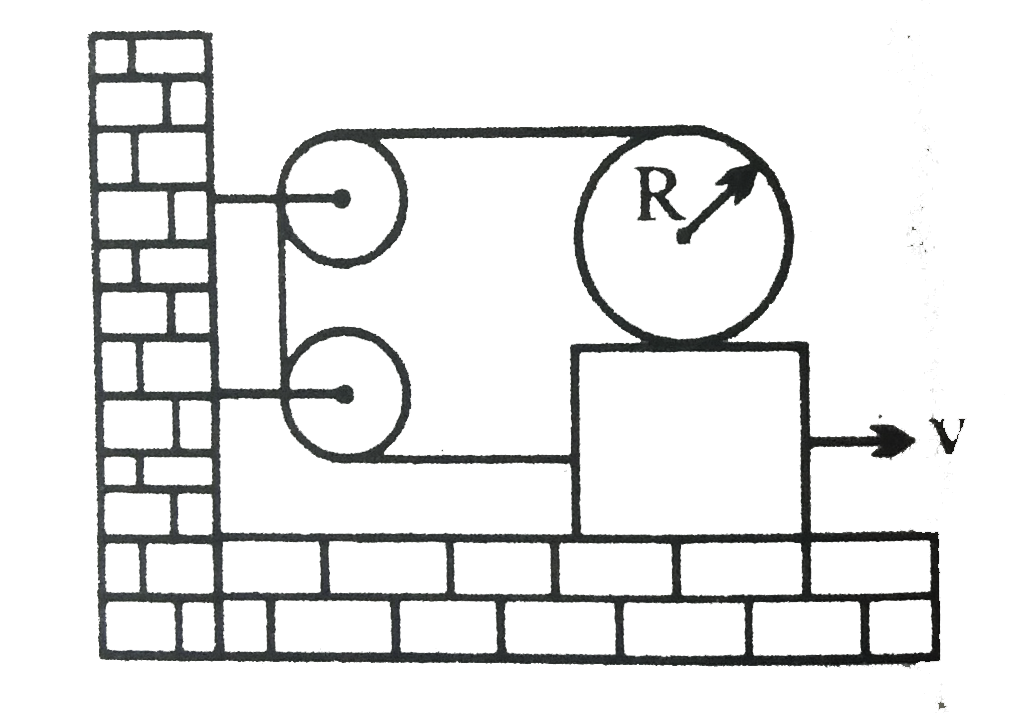 .Athe speed of the centre of mass of the cylinder is 2v.Bthe speed of the centre of mass of the cylinder is zero.Cthe angular velocity of the cylinder is v/R.Dthe angular velocity of the cylinder is zero.
.Athe speed of the centre of mass of the cylinder is 2v.Bthe speed of the centre of mass of the cylinder is zero.Cthe angular velocity of the cylinder is v/R.Dthe angular velocity of the cylinder is zero.A plank with a uniform sphere placed on it rests on a smooth horizontal plane. The plank is pulled to the right by a constant force F. It the sphere does not slip over the plank, then
 Aboth have the same accelerationBacceleration of the centre of sphere is less than that of the plankCwork done by friction acting on the sphere is equal to its total kinetic energyDtotal kinetic energy of the system is equal to work done by the force F
Aboth have the same accelerationBacceleration of the centre of sphere is less than that of the plankCwork done by friction acting on the sphere is equal to its total kinetic energyDtotal kinetic energy of the system is equal to work done by the force FA cylinder is rolling without slipping on a horizontal plane P. The friction between the plank P and the cylinder is sufficient for no slipping. The coefficient of friction between the plank and the ground surface is zero. Initially, P is attached with a string S as shown in the figure. If the string is now burned, then.
Athe plank with start motion with a speed v along forward direction.Bthe plank will start motion with a speed v along backward direction.Cthe plank will remain staticDlinear velocity of the cylinder will decrease and angular velocity will increase.
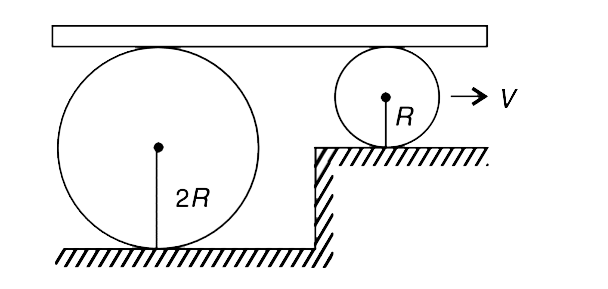
In the figure the plank resting on two cylinders is horizontal. The plank is pulled to the right such that the centre of smaller cylinder moves with a constant velocity v. Friction is large enough to prevent slipping at all surfaces. Find-
(a) The velocity of the centre of larger cylinder.
(b) The ratio of accelerations of the points of contact of the two cylinders with the plank.
View SolutionIn the figure shown a plank of mass m is lying at rest on a smooth horizontal surface. A cylinder of same mass m and radius r is rotated to an angular speed w0 and then gently placed on the plank. It is found that by the time the slipping between the plank and the cylinder cease, 50% of total kinetic energy of the cylinder and plank system is lost. Assume that plank is long enough and um is the coefficient of friction between the cylinder and the plank.
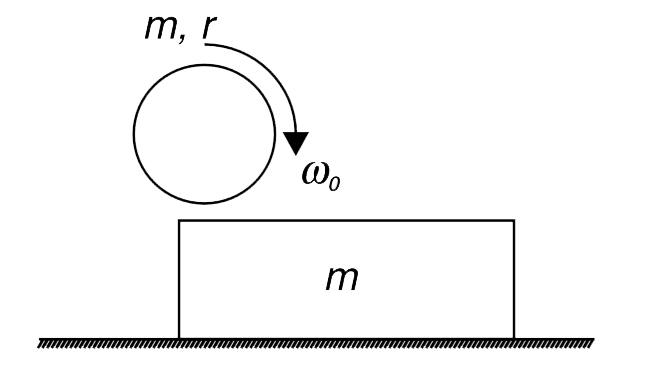
(a) Find the final velocity of the plank.
(b) Calculate the magnitude of the change in angular momentum of the cylinder about its centre of mass.
(c) Distance moved by the plank by the time slipping ceases between cylinder and plank.
View SolutionA solid cylinder of mass M and radius 2R is rolled up on an incline with the help of a plank of mass 2M as shown in the figure. A constant force F is acting on the plank parallel to the incline. There is no slipping at any of the contact. The friction force between the plank and cylinder is given by:

View SolutionThe acceleration a of the plank P required to keep the centre C of a cylinder in a fixed position during the motion is (no slipping take place between cylinder and plank)

View Solution
A cylinder of radius R is to roll without slippoing between two planks as shown in the figure. Then
View Solution
