(a) There is an infinitely long thread uniformly charged with linear charge density λC/m. Using Gauss’ law, calculate the electric field (E0) at a distance x from the thread. (b) Now consider a semi-infinite uniformly charged thread (linear charge density =λ) as shown in figure. Find the y component of electric field at point P in terms of E0. Use simple qualitative argument. (c) For the situation described in (b) calculate the x component of electric field at point P using the method of integration. (d) Find the angle that the electric field at P makes with x direction.
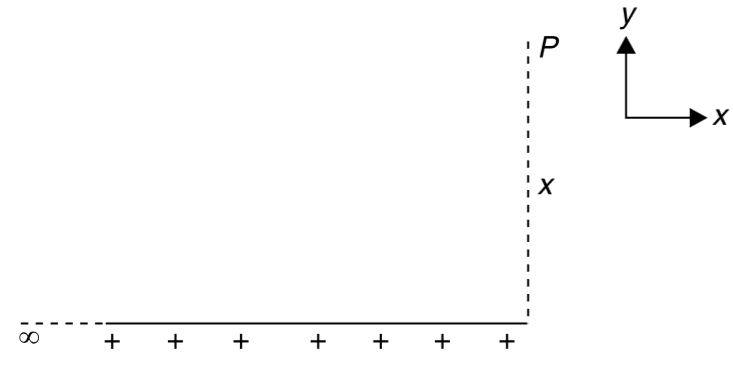
The correct Answer is:(a). E0=λ2πε0x
(b). Ey=E02
(c). Ex=E02=λ4πε0x
(d). 45∘
Similar Questions
Knowledge Check
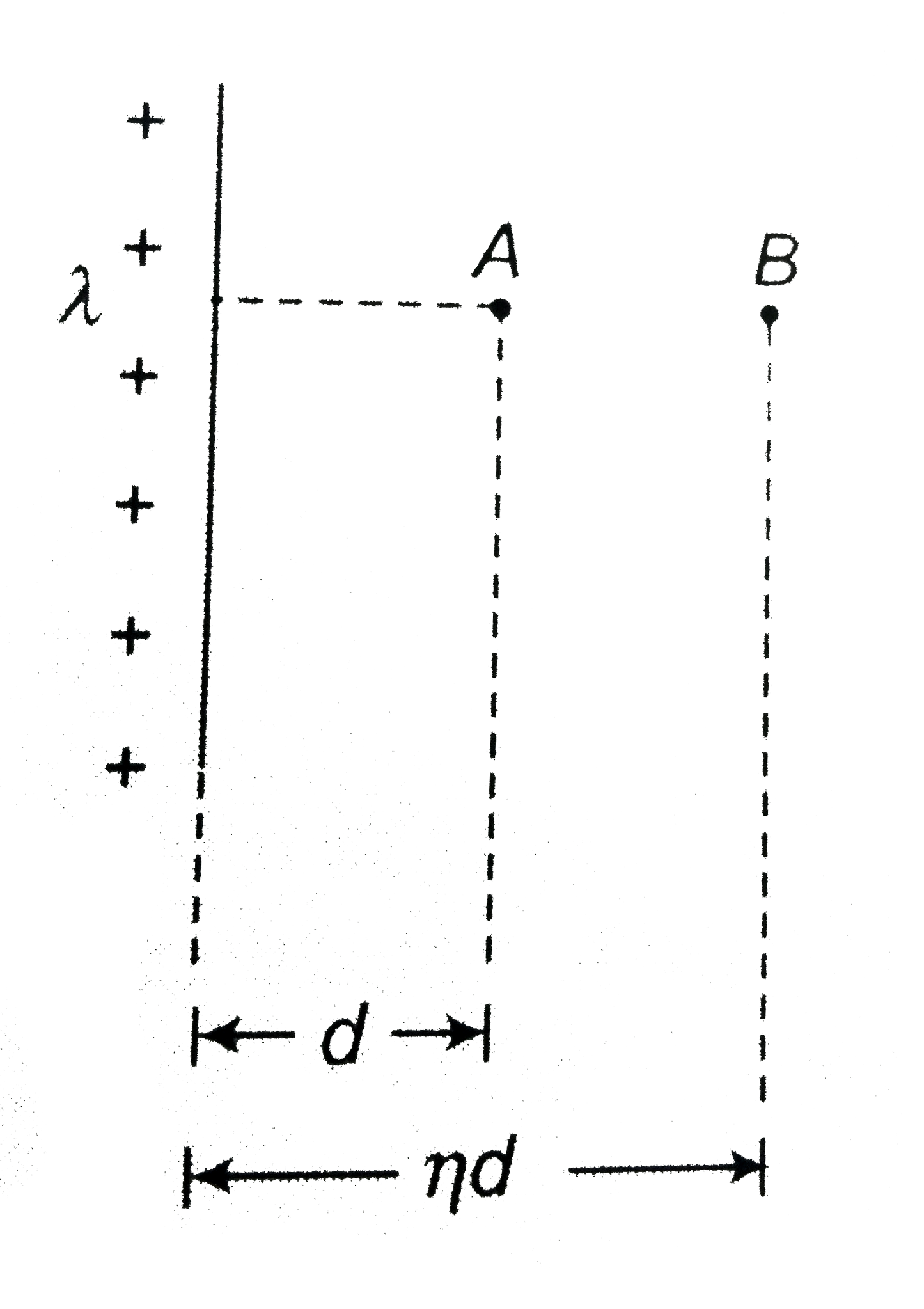
Find ratio of electric at point A and B. Infinitely long uniformly charged wire with linear charge density λ is kept along z-axis:
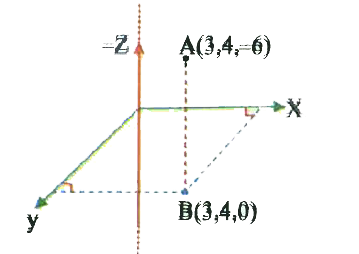 A1:2B1:6C6:1D1:1
A1:2B1:6C6:1D1:1An infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
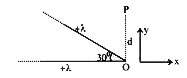 Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]
Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]
Find the total force on charge q due to a charge rod having linear charge density λCm placed as shown in figure.
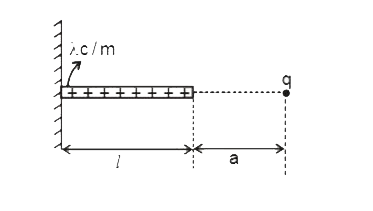
View SolutionFind the electric field intensity at a point P which is at a distance R (point lying on the perpendicular drawn to the wire at one of its end) from a semi-infinite uniformly charged wire. (Linear charge density = λ).
View SolutionFind the electric field intensity at a point P which is at a distance R (point lying on the perpendicular drawn to the wire at one of its end) from a semi-infinite uniformly charged wire. (Linear charge density = λ).
View SolutionIn the given arrangement find the electric field at C in the figure. Here the U-shaped wire is uniformly charged with linear charge density λ. [0]
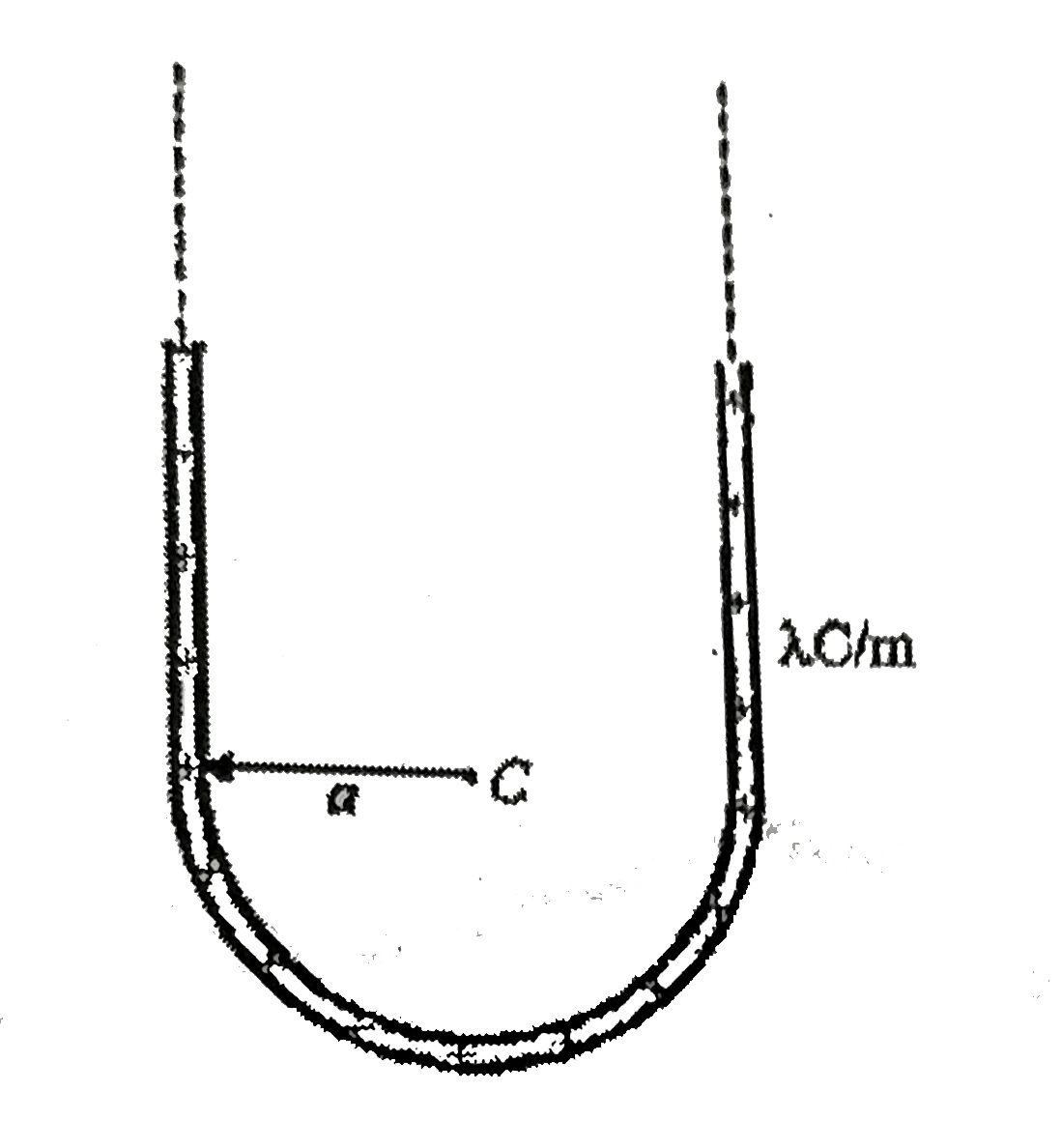
View SolutionAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :

View SolutionIntensity of electric field at a perpendicular distance of 0.5 m from an infinitely long line charge having linear charge density (λ) is 3.6×103Vm−1 . Find the value of λ
View Solution