सिद्ध करे कि ∣∣ ∣ ∣∣−a2abacba−b2bccacb−c2∣∣ ∣ ∣∣≥0 जहाँ a∈R,b∈R,c∈R
=4a2b2c2≥0
समान प्रश्न
If a+b+c=4 and a2+b2+c2+3(ab+bc+ac)=21 where a,b,c∈R then ab+bc+ca=
View Solutionयदि a,b,c ∈ R तब सारणिक △∣∣ ∣ ∣∣a2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2∣∣ ∣ ∣∣ अऋणांत्मक होगा पुनः सारणिक के शून्य होने के सार्थ बताये
View SolutionIf a,b,c and A,B,C ∈R-{0} such that aA+bB+cD+√(a2+b2+c2)(A2+B2+C2)=0, then value of aBbA+bCcB+cAaC is
View SolutionProve that: ∣∣ ∣ ∣∣−a2abacba−b2bccacb−c2∣∣ ∣ ∣∣=4a2b2c2
View SolutionProve that,∣∣ ∣ ∣∣−a2abacba−b2bccacb−c2∣∣ ∣ ∣∣=4a2b2c2.
View SolutionIf a,b,c and A,B,C in R-{0} such that aA+bB+cC-sqrt((a^(2)+b^(2)+c^(2))(A^(2)+B^(2)+C^(2)))=0 , then value of (aB)/(bA) +(bC)/(cB) + (cA)/(aC) is
View SolutionIn Fig, 2.38,
(a) is CA+CB=AB? (b) is BA+AC=CB ?
(c ) is AB+BC=CA ?
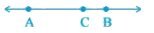
View SolutionLet Delta =|{:(-bc,b^(2)+bc,c^(2)+bc),(a^(2)+ac,-ac,c^(2)+ac),(a^(2)+ab,b^(2)+ab,-ab):}| and the equation x^(3)-px^(2)+qx-r=0 has roots a,b,c, where a,b,c in R^(+) The value of Delta is
View Solution

