Which of the following pairs of triangle are congruent? ABC:AB=10 cm, ∠A=400, ∠B=550;XYZ:XY=10,∠Y=400, ∠Z=850 PQR:PR=5 cm, ∠P=370, ∠R=640; DEF:DE=5 cm, ∠D=370, ∠F=640
To determine which pairs of triangles are congruent, we will analyze the given triangles using the Angle-Side-Angle (ASA) congruence criterion.
1. Identify the first pair of triangles:
- Triangle ABC:
- AB = 10 cm
- ∠A = 40°
- ∠B = 55°
- Triangle XYZ:
- XY = 10 cm
- ∠Y = 40°
- ∠Z = 85°
2. Calculate the missing angle in triangle XYZ:
- The sum of angles in a triangle is 180°.
- Therefore, ∠X = 180° - (∠Y + ∠Z) = 180° - (40° + 85°) = 180° - 125° = 55°.
3. Compare the angles and sides of triangles ABC and XYZ:
- Triangle ABC has angles: ∠A = 40°, ∠B = 55°, and the side AB = 10 cm.
- Triangle XYZ has angles: ∠Y = 40°, ∠Z = 85°, and the side XY = 10 cm.
- Since both triangles have two angles and the included side (AB and XY) equal, we can conclude:
- Triangle ABC is congruent to triangle XYZ by ASA congruence.
4. Identify the second pair of triangles:
- Triangle PQR:
- PR = 5 cm
- ∠P = 37°
- ∠R = 64°
- Triangle DEF:
- DE = 5 cm
- ∠D = 37°
- ∠F = 64°
5. Calculate the missing angle in triangle DEF:
- The sum of angles in a triangle is 180°.
- Therefore, ∠E = 180° - (∠D + ∠F) = 180° - (37° + 64°) = 180° - 101° = 79°.
6. Compare the angles and sides of triangles PQR and DEF:
- Triangle PQR has angles: ∠P = 37°, ∠R = 64°, and the side PR = 5 cm.
- Triangle DEF has angles: ∠D = 37°, ∠F = 64°, and the side DE = 5 cm.
- However, ∠E = 79° in triangle DEF does not equal ∠Q in triangle PQR (which is 79°).
- Since the angles do not match, we cannot conclude that triangle PQR is congruent to triangle DEF.
Conclusion:
- Triangle ABC is congruent to triangle XYZ (by ASA).
- Triangle PQR is not congruent to triangle DEF.
- Triangle ABC:
- AB = 10 cm
- ∠A = 40°
- ∠B = 55°
- Triangle XYZ:
- XY = 10 cm
- ∠Y = 40°
- ∠Z = 85°
- The sum of angles in a triangle is 180°.
- Therefore, ∠X = 180° - (∠Y + ∠Z) = 180° - (40° + 85°) = 180° - 125° = 55°.
- Triangle ABC has angles: ∠A = 40°, ∠B = 55°, and the side AB = 10 cm.
- Triangle XYZ has angles: ∠Y = 40°, ∠Z = 85°, and the side XY = 10 cm.
- Since both triangles have two angles and the included side (AB and XY) equal, we can conclude:
- Triangle ABC is congruent to triangle XYZ by ASA congruence.
- Triangle PQR:
- PR = 5 cm
- ∠P = 37°
- ∠R = 64°
- Triangle DEF:
- DE = 5 cm
- ∠D = 37°
- ∠F = 64°
- The sum of angles in a triangle is 180°.
- Therefore, ∠E = 180° - (∠D + ∠F) = 180° - (37° + 64°) = 180° - 101° = 79°.
- Triangle PQR has angles: ∠P = 37°, ∠R = 64°, and the side PR = 5 cm.
- Triangle DEF has angles: ∠D = 37°, ∠F = 64°, and the side DE = 5 cm.
- However, ∠E = 79° in triangle DEF does not equal ∠Q in triangle PQR (which is 79°).
- Since the angles do not match, we cannot conclude that triangle PQR is congruent to triangle DEF.
- Triangle ABC is congruent to triangle XYZ (by ASA).
- Triangle PQR is not congruent to triangle DEF.
Similar Questions
Which of the following pairs of triangles are congruent? ABC:AB=2 cm, AC=4 cm, ∠A=400;XYZ:XZ=YZ=4,∠Z=400 PQR:PQ=5 cm, PR=6 cm, ∠P=550; DEF:DE=6 cm, EF=5 cm, ∠D=550
View SolutionWhich of the following pairs of triangles are congruent? If they are congruent, write out the pairs of equal angles. ABC:AB=3cm, BC=4cm, CA=2 cm DEF:DE=2 cm, EF=3 cm and FD=4 cm PQR:PQ=17 cm, QR=15 cm, PR=18 cm DEF:DE=18 cm, EF=17 cm, DF=15 cm .
View Solution
Knowledge Check
Out of the following one which is correct for equilibrium state ?
(a) ΔG=0 (b) ΔS=0 (c ) rf=rb (d) Ecell=0Aa,bBonly bCa,c & dDonly c
If ABC and DEF are two triangles such that ABC ≅FDE and AB=5cm, ∠B=400 and ∠A=800. Then, which of the following is true? DF=5cm, ∠F=600 (b) DE=5cm, ∠E=600 DF=5 cm, ∠E=600 (d) DE=5cm, ∠D=400
View SolutionIn a rhombus ABCD, if ∠ACB=40∘, then ∠ADB=(a) 70∘ (b) 45∘ (c) 50∘ (d) 60∘
View SolutionIn Figure, if AB∣∣CD, ∠APQ=500AND ∠PRD=1270, find x and y
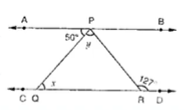
View SolutionIn a parallelogram ABCD, if ∠A=(3x−20)∘,∠B=(y+15)∘,∠C=(x+40)∘, then find the values of xandy
View SolutionIn Fig.102, ABCDEF, ∠ABG=1100,∠GCD=1000 and ∠BGC=x0. the value of x is (a) 35 (b) 50 (c) 30 (d) 40
View SolutionIn fig. 15,D,E are points on sides AB, AC of ABC such that DE∣∣BC. if ∠B=300 and ∠A=400, find x0,y0,z0.
View SolutionABCD is a cyclic quadrilateral in which: BCAD, ∠ADC=1100 and ∠BAC=500. Find ∠DAC ∠DBC=800 and ∠BAC=400. Find ∠BCD ∠BCD=1000and ∠ABD=700 find ∠ADB
View Solution
