If f(x)=2x−3, the inverse of f,f−1 could be represented by
f−1(x)=3x−2
f−1(x)=12x−3
f−1(x)=x−23
f−1(x)=x+32
The correct Answer is:D
To find the inverse of the function f(x)=2x−3, we will follow these steps:
1. Replace f(x) with y:
y=2x−3
2. Isolate x:
- First, add 3 to both sides:
y+3=2x
- Next, divide both sides by 2:
x=y+32
3. Express the inverse function:
- We can now express the inverse function f−1(x) by replacing y with x:
f−1(x)=x+32
Final Answer:
Thus, the inverse of the function f(x)=2x−3 is:
f−1(x)=x+32
y=2x−3
- First, add 3 to both sides:
y+3=2x
- Next, divide both sides by 2:
x=y+32
- We can now express the inverse function f−1(x) by replacing y with x:
f−1(x)=x+32
Thus, the inverse of the function f(x)=2x−3 is:
f−1(x)=x+32
Similar Questions
Knowledge Check
If f(x)=x, the inverse of f,f−1, could be represented by
Af−1(x)=xBf−1(x)=1Cf−1(x)=1xDf−1(x)=yIf f(x)=x3−4, then the inverse of f=
A−x3+4B3√x+4C3√x−4D1x3−4If f(x)=1−4x, and f−1(x) is the inverse of f(x), then f(−3)f−1(−3)=
A1B3C4D13
If f(x)=x3+2x2+3x+4 and g(x) is the inverse of f(x) then g′(4) is equal to- 14 (b) 0 (c) 13 (d) 4
View SolutionIf y=f(x)=x3+x5 and g is the inverse of f find g′(2)
View SolutionLet f:A→Bf(x)=x+abx2+cx+2, where A represent domain set and B represent range set of function f(x) a,b,c ∈R,f(−1)=0andy=1 is an asymptote of y=f(x)andy=g(x) is the inverse of f(x).
Area of region enclosed by asymptotes of curves y=f(x)andy=g(x) is:
View SolutionLet F:[3,∞]→[1,∞] be defined by f(x)=πx(x−3), if f−1(x) is inverse of f(x) then the number of solution of the equation f(x)=f−1(x) are
View SolutionThe graph of y=f(x) is shown below.
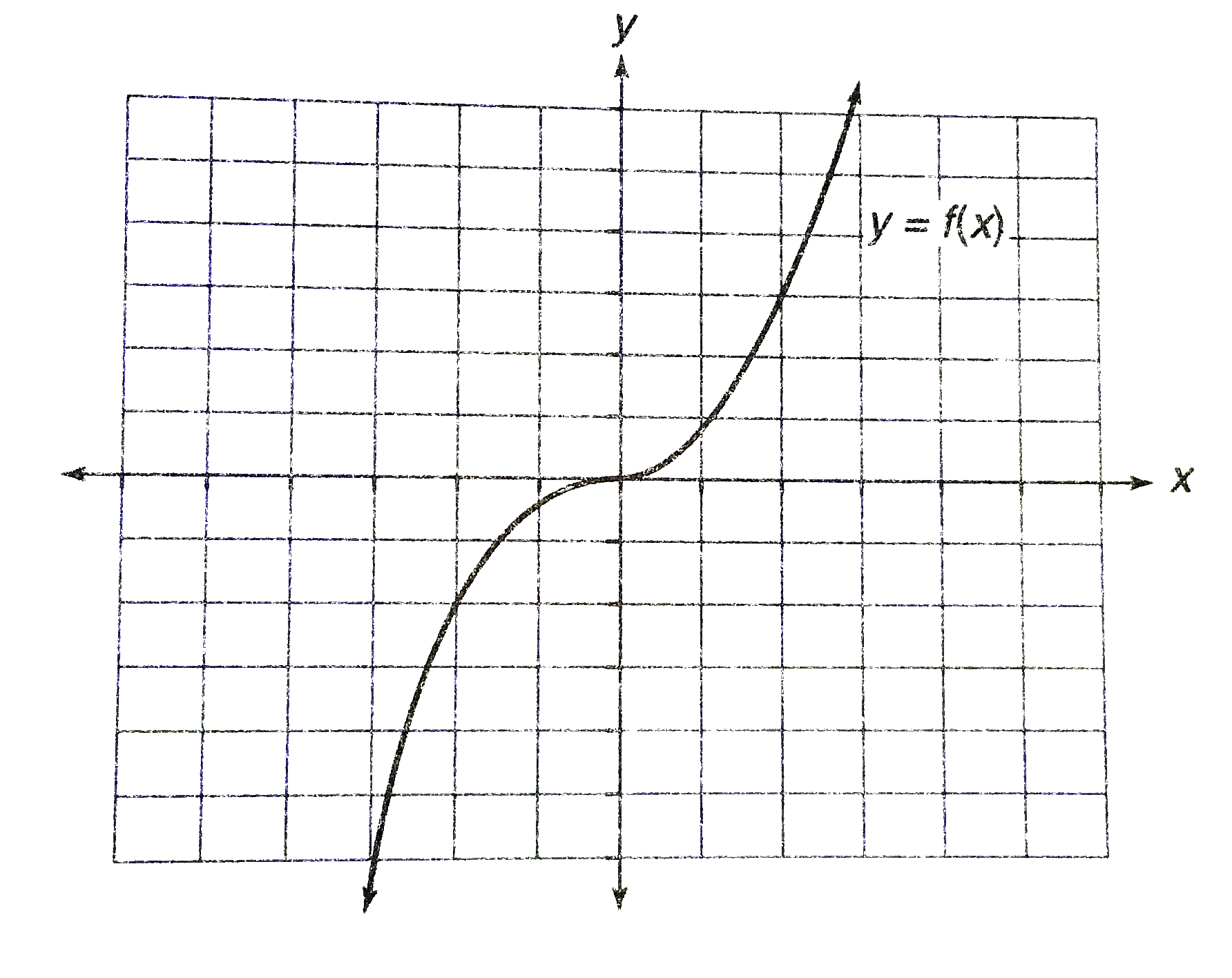
Which of the following could represents the graph of y=f(x−2)+1?
View Solution
