In a factory, the production of scooters rose to 46305 from 40000 in 3 years. Find the annual rate of growth of the production of scooters.
To find the annual rate of growth of the production of scooters in a factory, we can use the formula for compound interest. The formula is:
A=P(1+R100)N
Where:
- A = the amount after time N (final value)
- P = the principal amount (initial value)
- R = the annual rate of growth (which we need to find)
- N = the number of years
Step 1: Identify the values
From the problem:
- Initial production P=40000
- Final production A=46305
- Number of years N=3
Step 2: Substitute the values into the formula
We substitute the known values into the formula:
46305=40000(1+R100)3
Step 3: Divide both sides by 40000
To isolate the term with R, we divide both sides by 40000:
4630540000=(1+R100)3
Calculating the left side:
4630540000=1.157625
So, we have:
1.157625=(1+R100)3
Step 4: Take the cube root of both sides
To solve for 1+R100, we take the cube root of both sides:
1+R100=√(3)1.157625
Calculating the cube root:
√(3)1.157625≈1.05
Step 5: Isolate R
Now, we isolate R:
R100=1.05−1
R100=0.05
Step 6: Multiply by 100 to find R
To find R, multiply both sides by 100:
R=0.05×100
R=5
Conclusion
The annual rate of growth of the production of scooters is 5%.
---
- A = the amount after time N (final value)
- P = the principal amount (initial value)
- R = the annual rate of growth (which we need to find)
- N = the number of years
From the problem:
- Initial production P=40000
- Final production A=46305
- Number of years N=3
We substitute the known values into the formula:
To isolate the term with R, we divide both sides by 40000:
To solve for 1+R100, we take the cube root of both sides:
Now, we isolate R:
To find R, multiply both sides by 100:
The annual rate of growth of the production of scooters is 5%.
Similar Questions
Knowledge Check
In a factory, the production of cycles rose to 48,400 from 40,000 in 2 years. The rate of growth per annum is
A0.09B0.08C0.105D0.1In which year was the total production of scooters the maximum?
A1989B1986C1987D1995In India there were only three bicycle making companies in the given period. The following table shows the production of units (in 000)

The simple average rate of growth of production of Hero cycles from 1990-95 :A37%B42%C27%D31.5%
A factory increased its production of three wheelers from 80000 in 1999 to 92610 in 2002. Find the annual rate of growth of production of three wheelers.
View SolutionA sum of money becomes 720 in 2 years and 1125 4 years. Find the annual rate of compound interest.
View SolutionThe production of electric bulbs in different factories is shown in the following table. Find the median of the productions.
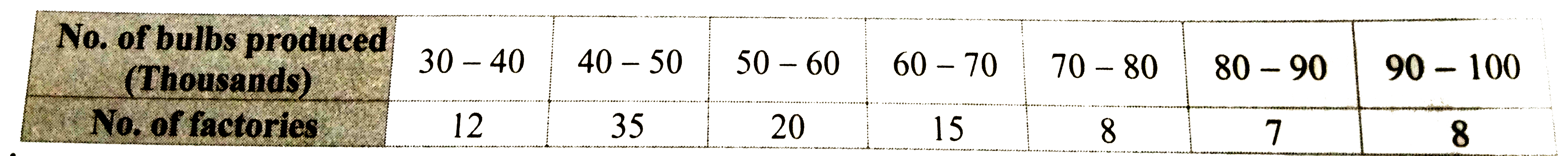
View SolutionThe ratio of the production of scooters by factoryP to that by factory T in 1985 is
View SolutionIn which year was the total production of scooters of all factories 20% of the total production of scooters during 1985−1989?
View Solution
