Three coherent point sources S1,S2andS3 are placed on a line perpendicular to the screen as shown in the figure. The wavelength of the light emitted by the sources is lambda. The distance between adjacent sources is d=3λ The distance of S2 from the screen is D(>>λ). Find the minimum (non zero) distance x of a point P on the screen at which complete darkness is obtained.

2√2D7
√(17)D8
4√5D
4√2D7
The correct Answer is:B
for nearest minima
dsinθ=8λ/3(i.e.2λ/3+λ+λ)⇒3λsinθ=8λ/3⇒sinθ=8/9
⇒tanθ=D/x=8√17⇒x=√17D8
Similar Questions
Two coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 is
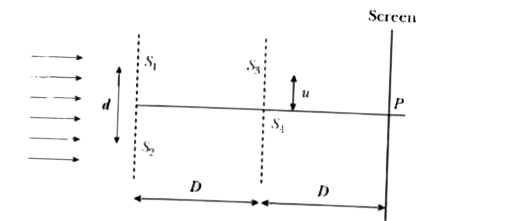
View SolutionIn the arrangement shown in the following figure, the wavelength of light used is λ. The distance between slits S1 and S2 is d (« D). The distance between S3 and S4 is u=λD/3d. If the ratio of maximum to minimum intensity observed on screen is k. Find k.
View Solution
Knowledge Check
Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 ApointsBstraight linesCsemi-circlesDconcentric circles
ApointsBstraight linesCsemi-circlesDconcentric circlesTwo coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
 Astraigth linesBsemi-circleCconcentric circlesDpoints
Astraigth linesBsemi-circleCconcentric circlesDpointsTwo coherent light sources S1 and S2(λ=6000Å) are 1mm apart from each other. The screen is placed at a distance of 25cm from the sources. The width of the fringes on the screen should be
A(a) 0.015cmB(b) 0.025cmC(c) 0.010cmD(d) 0.030cm
In a standard YDSE setup if the screen is kept tilted as shown, find the distance OA if first maximum is formed at A. Wavelength of light emitted by source is λ

View SolutionIn Young's double slit experiment, the distance between sources is 1mm and distance between the screen and source is 1 m . If the fringe width on the screen is 0.06cm , then λ=
View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance L. Each sources emits light of wavelength λ, where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Then
View SolutionIn Young's double-slit experiment using λ=6000Å, distance between the screen and the source is 1m. If the fringe-width on the screen is 0.06 cm, the distance between the two coherent sources is
View SolutionThe distance between two coherent sources is 1 mm. The screen is placed at a distance of 1 m from the sources. If the distance of the third bright fringe is 1.2 mm from the central fringe, the wavelength of light used is
View Solution

