Initially two particles A and B are present at (0,0) and (d,0) respectively They start moving with speed VA=Vˆi+Vˆj and VB=−Vˆj If R is magnitude of relative separation between them and T0 be the time when separation between them is minimum, then
T0=d5V
Rmin=2d√5
Graph of R versus time is straight line
Graph of R versus time is circle.
The correct Answer is:A, B
To solve the problem, we will follow these steps:
Step 1: Define the initial positions and velocities
- Particle A is at position (0,0) and moves with velocity VA=V^i+V^j.
- Particle B is at position (d,0) and moves with velocity VB=−V^j.
Step 2: Determine the relative velocity
The relative velocity of A with respect to B is given by:
VAB=VA−VB
Substituting the values:
VAB=(V^i+V^j)−(0^i−V^j)=V^i+2V^j
Step 3: Calculate the magnitude of the relative velocity
The magnitude of the relative velocity VAB is:
|VAB|=√(V)2+(2V)2=√V2+4V2=√5V2=V√5
Step 4: Find the time T0 when the separation is minimum
To find the time when the separation is minimum, we need to determine the perpendicular distance from particle B to the line of motion of particle A. The minimum distance occurs when the line connecting A and B is perpendicular to the direction of VAB.
The distance D between the initial positions of A and B is d. The time T0 to reach the minimum separation is given by:
T0=Dcosα|VAB|
Where cosα=1√5 (from the triangle formed by the components of VAB):
T0=d⋅1√5V√5=d5V
Step 5: Calculate the minimum separation Rmin
The minimum separation occurs when the perpendicular distance from particle B to the line of motion of A is given by:
Rmin=Dsinα
Where sinα=2√5 (using the triangle formed by the components of VAB):
Rmin=d⋅2√5=2d√5
Final Results
- The time T0 when the separation is minimum is:
T0=d5V
- The minimum separation Rmin is:
Rmin=2d√5
- Particle A is at position (0,0) and moves with velocity VA=V^i+V^j.
- Particle B is at position (d,0) and moves with velocity VB=−V^j.
The relative velocity of A with respect to B is given by:
VAB=VA−VB
Substituting the values:
VAB=(V^i+V^j)−(0^i−V^j)=V^i+2V^j
The magnitude of the relative velocity VAB is:
|VAB|=√(V)2+(2V)2=√V2+4V2=√5V2=V√5
To find the time when the separation is minimum, we need to determine the perpendicular distance from particle B to the line of motion of particle A. The minimum distance occurs when the line connecting A and B is perpendicular to the direction of VAB.
T0=Dcosα|VAB|
Where cosα=1√5 (from the triangle formed by the components of VAB):
T0=d⋅1√5V√5=d5V
The minimum separation occurs when the perpendicular distance from particle B to the line of motion of A is given by:
Rmin=Dsinα
Where sinα=2√5 (using the triangle formed by the components of VAB):
Rmin=d⋅2√5=2d√5
- The time T0 when the separation is minimum is:
T0=d5V
- The minimum separation Rmin is:
Rmin=2d√5
Similar Questions
Find out speed of particles when separation between them is r.

View SolutionTwo particles are located on a horizontal plane at a distance 60m. At t=0 both the particles are simultaneously projected at angle 45∘ with velocities 2ms−1and14ms−1, respectively. Find
(a) Minimum separation between them during motion.
(b) At what time is the separation between them minimum ?
 .
.
View Solution
Knowledge Check
Two particles A and B locat at (0,0) and (4,4) respectively start moving simu lataneou ly with velocities vA=−4ˆi and VB=−4ˆj:
Athe shortest distance between them is 4√2mBthe shortest distance between them first decreases and then increasesCthe distance between them increases from the beginningDthe magnitude of relative velocity of A w.r.t. B is 4m/sTwo projectile A and B located at (0,0) and (4.4) respectively start moving simu ltaneou lsy with velocities VA=−4ˆi and VB=4ˆj:
Athe shortest distance between them is 4√2mBthe shortest distance between them first decreases and then increasesCthe distance between them increases from the beginningDthe magnitude of relative velocity of A w.r.t. B is 4m/sParticles A and B are moving with constant velocities along x and y axis respectively, the graph of separation between them with time is
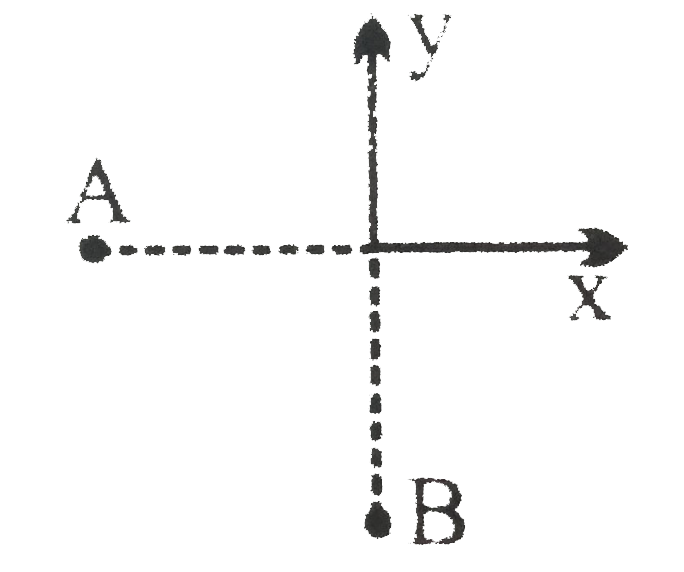 A
A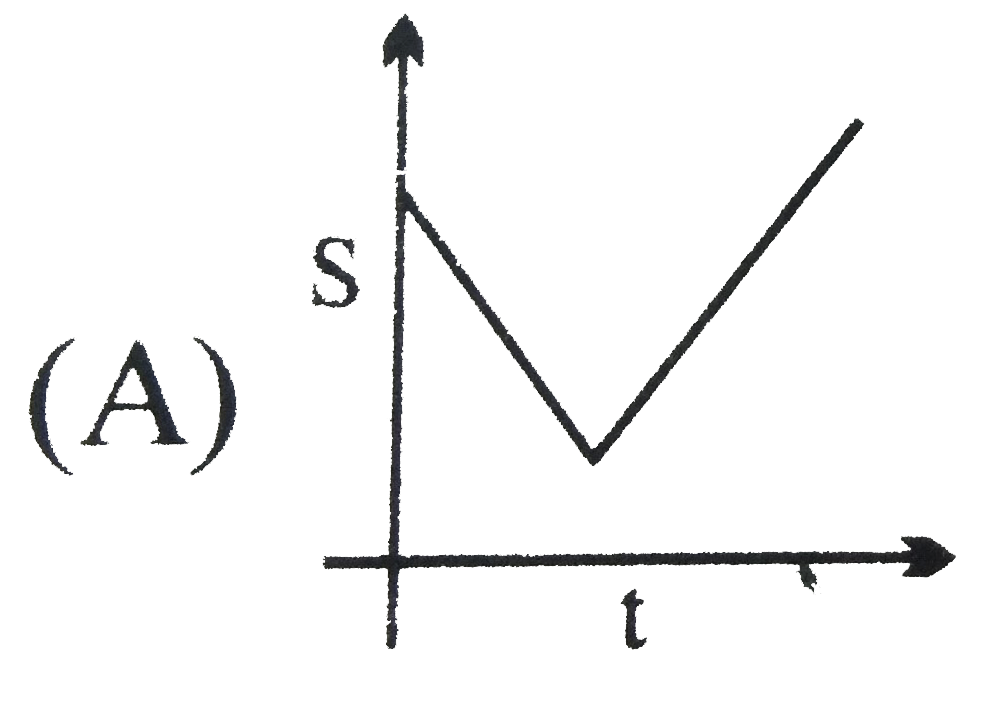 B
B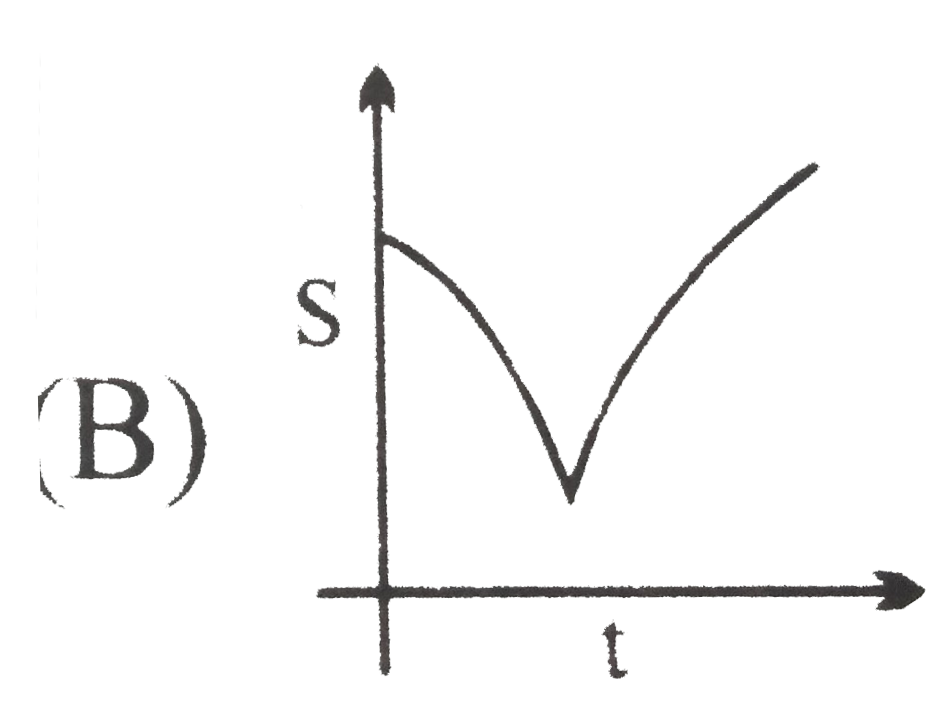 C
C D
D
In the figure shown in text, m1=m, m2=2m and initial distance between them is r0. Find velocities of the masses when separation between them becoms r02.
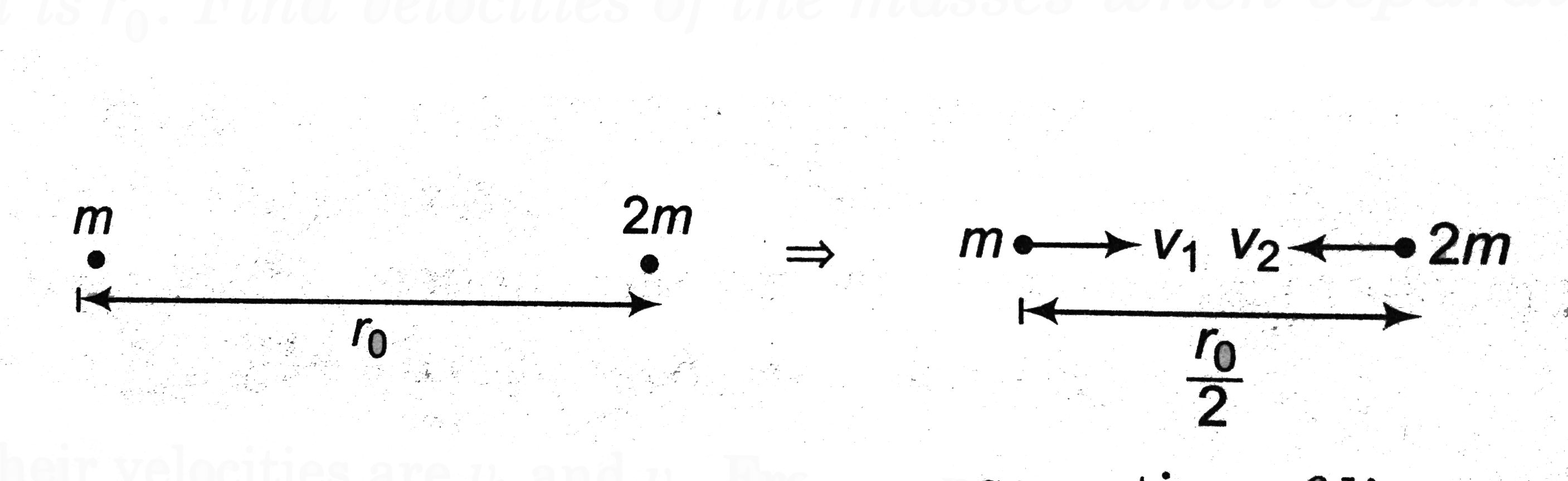
View SolutionTwo carts (A & B) having spring bumpers collides as shown in figure. Initially v1≠0 & v2=0. When the separation between the carts is minimum.

View Solution(a) Two protons are placed at separation d on a smooth surface. Find the speed of each proton when separation between them is doubled.
(b) An α-particle and a proton are placed at a separation d on a smooth surface.Find the speed of each when separation between them becomes infinite. (m: mass of proton , e: charge of proton.)
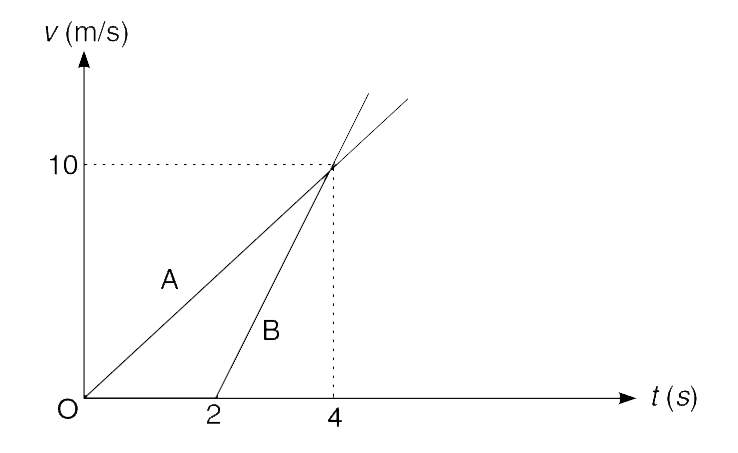
View SolutionTwo particles A and B start from same point and move along a straight line. Velocity-time graph for both of them has been shown in the fig. Find the maximum separation between the particles in the interval 0<t<5 sec.
View SolutionTwo particles start moving simultaneously from points (0, 0) and (1, 0) respectively in the OXY plane with uniform velocities v1 and v2 as shown in the figure. It is found that they collide. Then

View Solution

