A heavy particle is attached to one end of a string 1m long whose other end is fixed at O. It is projected from it lowest position horizontally with a velocity V:
If V2>5 g the particle will describe complete circular motion in the vertical plane
If V2=3.5 g the tension in the string will become zero after the string has turned through 120∘
If V2=2 g, the tension in the string becomes zero the velocity of the particle also becomes zero
If V2=g the velocity of the particle becomes zero after the string turns through 60∘
The correct Answer is:A, B, C, D
−mgl(1−cosθ)=12mv2−12mv2.......(1)
T−mgcosθ=ml2l.........(2)
V2=(2−3cosθ)
(A)θ=π,V2=5glhence true
(B) 3.5=2−3cosθ,cosθ=−12⇒θ=120∘hence true
(C) 2=2−3cosθ,cosθ=0,θ⇒π/2 hence true
(D) 1=2−3cosθ,cosθ=13,θ>60∘ hence true
Similar Questions
A heavy particle is attached to one end of a light string of length l whose other end is fixed at O. The oarticle is projectyed horizontally with a velocity v0 from its lowest position A. When the angular displacement of the string is more than90∘, the particle leaves the circular path at B. The string again becomes taut at C such that B,O,C are collinear. Find v0 in terms of l and g
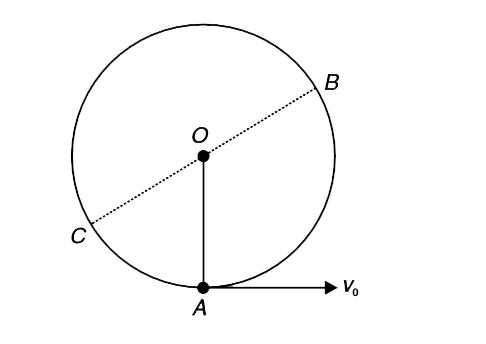
View SolutionA heavy particle is suspended by a light thread, the other end of the thread being fixed to a point O. The particle is projected from its lower position in the horizontal direction in the vertical plane through O, with such a velocity that it leaves the circular path after an angular displacement θ Show that when the string again becomes taut it makes an angle 3θ−360∘ with the downward drawn vertical.
View Solution
Knowledge Check
A particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u. The tension in the string T and acceleration of the particle is a any position. Then T is zero at highest point if
Au>√5glBu=√5glCBoth (a) and (b) are correctDBoth (a) and (b) are wrongA partical is moving in the vertical plane . It is attached at one end of a string of length l whose other end is fixed. The velocity at the lower point is u. The tension in the string is →T and velocity of the partical is →v at any position. Then, which of the following quantity will remain constant.
A→T.→vBkinetic energyCGravitational potential energyD→T×→vA particle of mass m is attached to one end of a string of length l while the other end is fixed to a point h above the horizontal table. The particle is made to revolve in a circle on the table so as to make p revolutions per second. The maximum value of p if the particle is to be in contact with the table will be :
A2π√ghB√g/hC2π√h/gD12π√g/h
A small ball of mass m is attached to the end of the string of length l=1 m whose other end is fixed. From its lowest position, the ball is given a kinetic energy ml/5. the net acceleration (in m/s2) of the ball at the instant when the string makes an angle θ of 37∘C with the downwards vertical is___________
View SolutionA heavy particle is tied ot the end A of a string of length 1.6m. Its other end O is fixed. It revolves as a conical pendulum with the string making 60∘ with the vertical. Then (g=10m/s2)
View SolutionA heavy particle is tied to the end A of a string of length 1.6 m. its other end O is fixed. It revolves as a conical pendulum with the string making 60C with the vertical then (g=10ms2)
View SolutionA mass is attached to the end of a string of length l which is tied to a fixed point O. The mass is released from the initial horizontal position of the string. Below the point O at what minimum distance a peg P should be fixed so that the mass turns about P and can describe a complete circle in the vertical plane?
View SolutionA small block of mass m is attached to free end of a spring of force cosntant k , whose other end is fixed to a rigid support . The block is lying on a frictionless horizontal plane and it starts movi0ng away from fixed end of the spring a\t t= 0 with intial velocity u When the speed of the block is 0.6μ it collides with a fixed heavy mass elastically. After the collision with a fixed heavy mass elastically . Aftere the collision the time at which the block passes through its equilibrium position for the first time is close to
View Solution

