A particle P is to be projected from a fixed point A on the ground with a fixed speed u. Another particle Q is also to be projected from a point B which is directly above the point A. The trajectory of the particle Q touches all possible trajectories (for different angle of projection) of the particle P in the vertical x−y plane. Find the equation of trajectory of the particle Q. (Take the point A as origin, horizontal axis x− axis and vertical axis y−axis Consider the figure.)

In order for the trahectory of Q to touch that of P when the latter is projected vertically upward, Q must be projected horizontally from the highest point. To visualize this, consider the trajectories of P as the angle of projection of P(θ,say), approaches 90∘ (i.e. for vertical projection).Let Q be projected horizontally from B with a speed v, where A=u32g. The point of impact of Q on the horizontal plane represents the point of maximum range for P along the horizontal.
OC=u2g=v√2hg, where h=u22g
i.e., v=u
The trajectory of Q is
u22g−y=12gt2. where t=x/v(v≡u)

Similar Questions
Two particles P and Q are projected from two points in the same plane as shown. Find the condition for collision of two paricles.
View SolutionA particle of mass m is projected from the ground with an initial speed u at an angle α. Find the magnitude of its angular momentum at the highest point of its trajector about the point of projection.
View Solution
Knowledge Check
The ratio of the speed of a projectile at the point of projection to the speed at the top of its trajectory is x. The angle of projection with the horizontal is
Asin1xBcos−1xCsin−1(1/x)Dcos−1(1/x)A particle is projected vertically upward with velocity u from a point A, when it returns to the point of projection .
AIts average speed is u/2.BIts average velocity is zero.CIts displacement is zero.DIts average speed is u.A particle is projected from point A on the ground at an angle θ with horizontal. Another particle is projected from point B simultaneously from height 4H above point A with same velocity A and B are in the same vertical plane, where H is the maximum height attained by the particle A, Both the particle collide at the same time on the ground. Find the angle at which particle B is projected with hoizontal.
Aθ upwardsBθ downwardsCzeroDNone of these
A particle is projected from a point on the level ground and its height is h when at horizontal distances aand2a from its point of projection. Find the velocity of projection.
View SolutionA particle is projected with a velocity →v=aˆi+bˆj. Find the radius of curvature of the trajectory of the particle at the (f) point of projection (ii) highest point.
View SolutionA particle is projected from the ground with an initial speed of v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
View Solution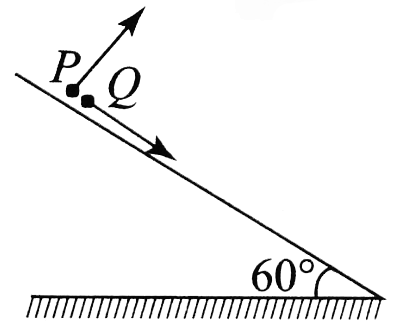
A particle P is projected from a point on the surface of smooth inclined plane (see figure). Simultaneously another particle Q is released on the smooth inclined plane from the same position. P and Q collide aftert=4. The speed of projection of P is
View SolutionA particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
View Solution

