A small coin is placed on a stationery horizontal disc at a distance r from its centre. The disc starts rotating about a fixed vertical axis through its centre with a constant angular acceleration α. Determine the number of revolutions N, accomplished by the disc before the coin starts slipping on the disc. Find the coefficient of static friction between the coin and the disc is μ9.
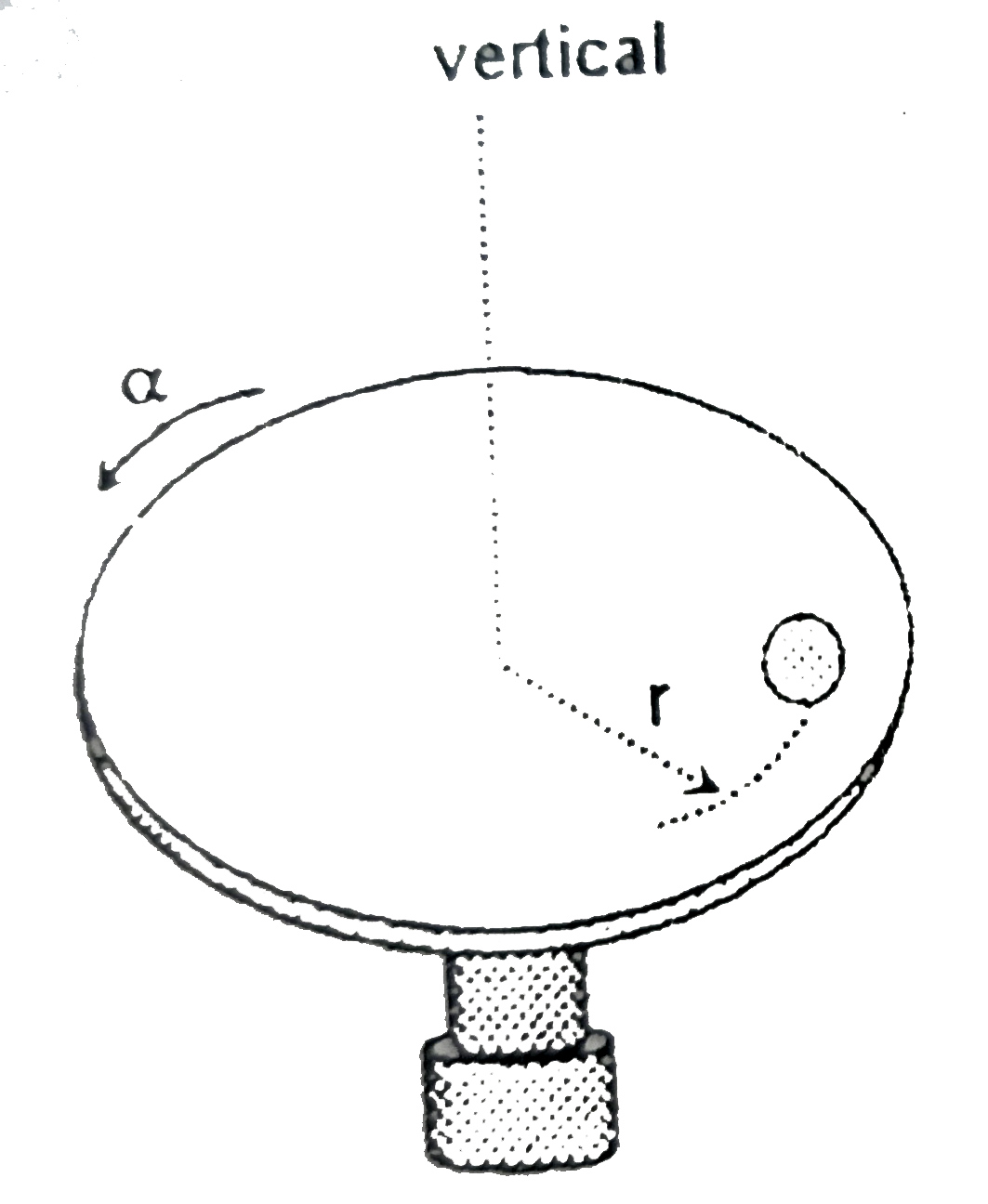
we draw the FBD of the coin
fT= tangential component of frictional force on coin
fR= radial component of frictional force on coin s
fT=mαr
fr=mω2fr
√f2R+f2T≤μgmg
2πN=ω2f2α
Solving the equations, we get
N=(μggr−α2)1/24πα
Similar Questions
A coin placed on a horizontal rotating disc, with its centre at 10 cm from the centre of the disc, is about to slip off when the disc performs 60 rpm. Find the coefficient of friction between the coin and the disc.
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View Solution
Knowledge Check
A coin is placed on the horizontal surface of a rotation disc. The distance of the coin from the axis is 1 m and coefficient of friction is 0.5. If the disc starts from rest and is given an angular acceleration 1√2 rad /sec2, the number of revolutions through which the disc turns before the coin slips is
A4πB74πC54πD34π
A horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is μs .Find the velocity of the before it start sliding relative as the disc

View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is μs .Find the velocity of the before it start sliding relative as the disc

View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is μs .Find the velocity of the before it start sliding relative as the disc

View SolutionA disc rotates about its aixs of symmetry in a horizontal plane at a steady rate of 3.5 revolutions per second A coin placed at a distance fo 1.25 cm form the axis of ratation remains at rest on the disc The coefficient of friction between the coin and the disc is : (g=10/s2)
View SolutionA disc rotates about its aixs of symmetry in a horizontal plane at a steady rate of 3.5 revolutions per second A coin placed at a distance fo 1.25 cm form the axis of ratation remains at rest on the disc The coefficient of friction between the coin and the disc is : (g=10/s2)
View SolutionA coin is placed on the horizontal surface of a rotation disc. The distance of the coin from the axis is 1 m and coefficient of friction is 0.5. If the disc starts from rest and is given an angular acceleration 1√2 rad /sec2, the number of revolutions through which the disc turns before the coin slips is
View Solution

