Three spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming "Head on" inelastic impact between B and C, we can 't conserve kinetic energy of entire system.
Velocity of A immediately after collision is along unit vector

ˆi
12ˆi+√32ˆj
ˆj
Cant't predict
Hint : Use impulse-momentum theorem along the rope and conservation of momentum perpendicular to the rope.
Similar Questions
Three spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming 'head on' inelastic impact between B and C, we cannot conserve kinetic energy of the entire system.
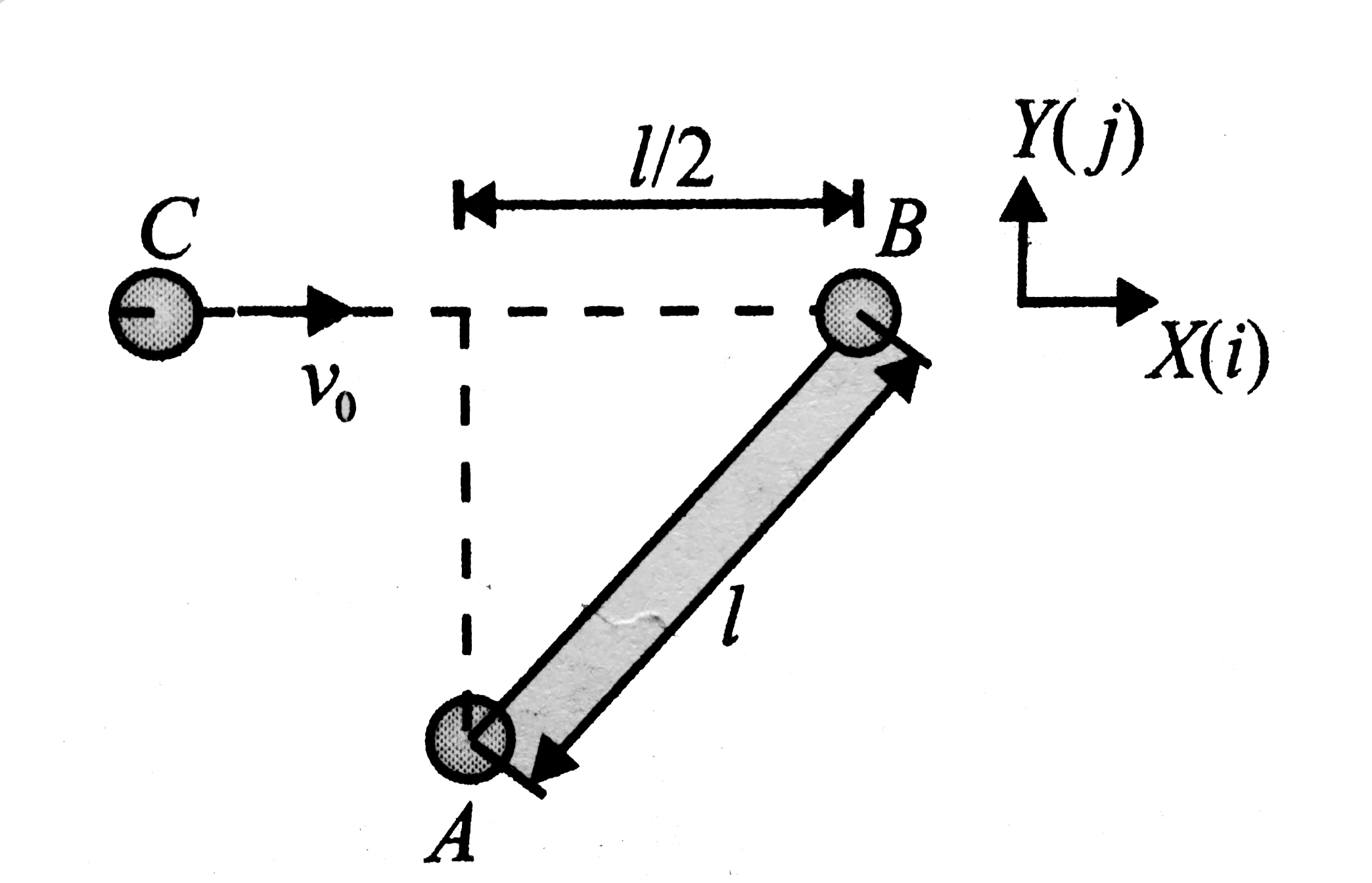
The magnitude of velocity of A immediately after collision is
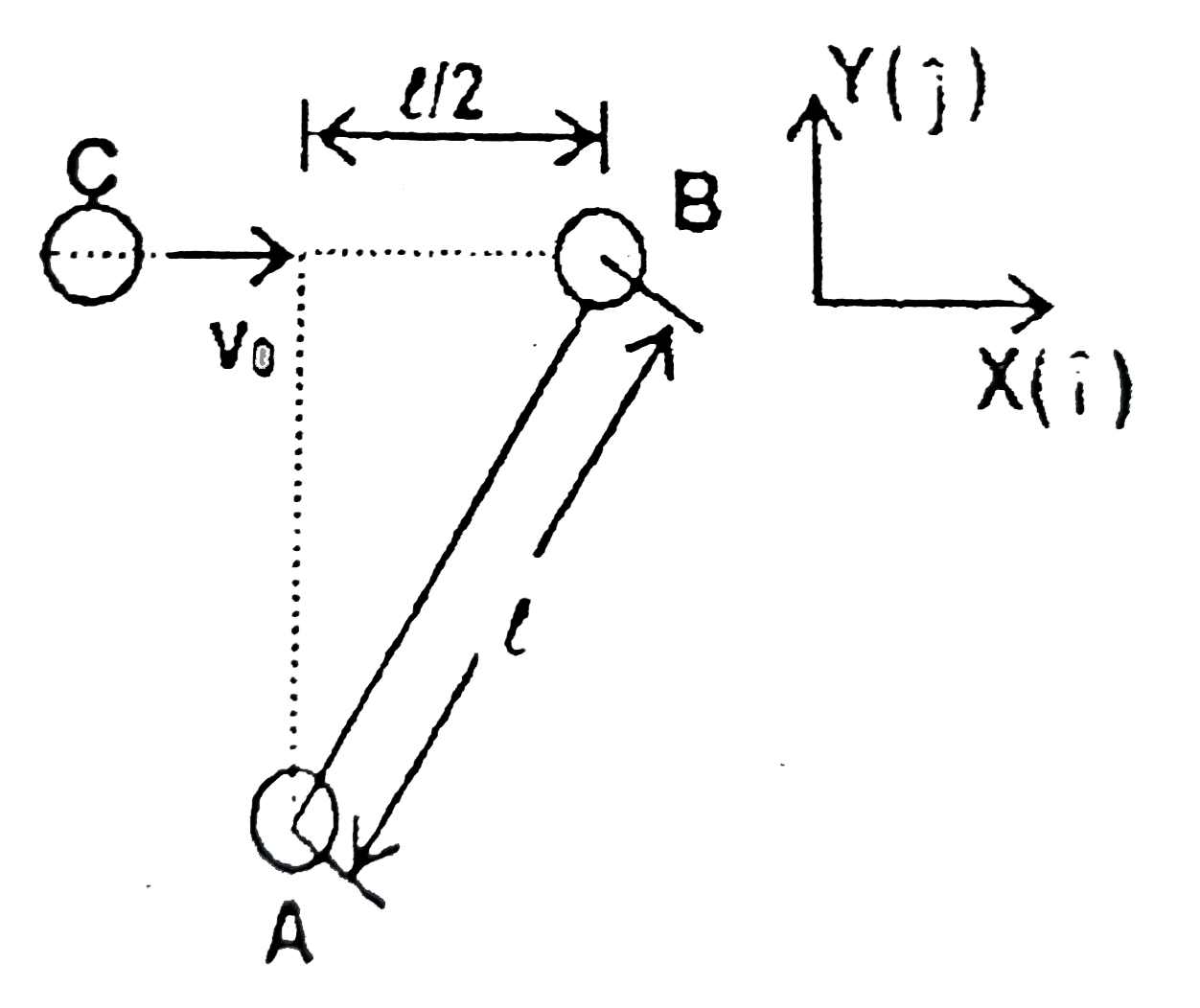
View SolutionThree spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming "Head on" inelastic impact between B and C, we can 't conserve kinetic energy of entire system.
If velocity of C immediately after collision becomes v02 in the initial direction of motion, the impulse due to string on sphere A is
View Solution
Knowledge Check
Three spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming "Head on" inelastic impact between B and C, we can 't conserve kinetic energy of entire system.
The velocity of B immediately after collision is along unit vector
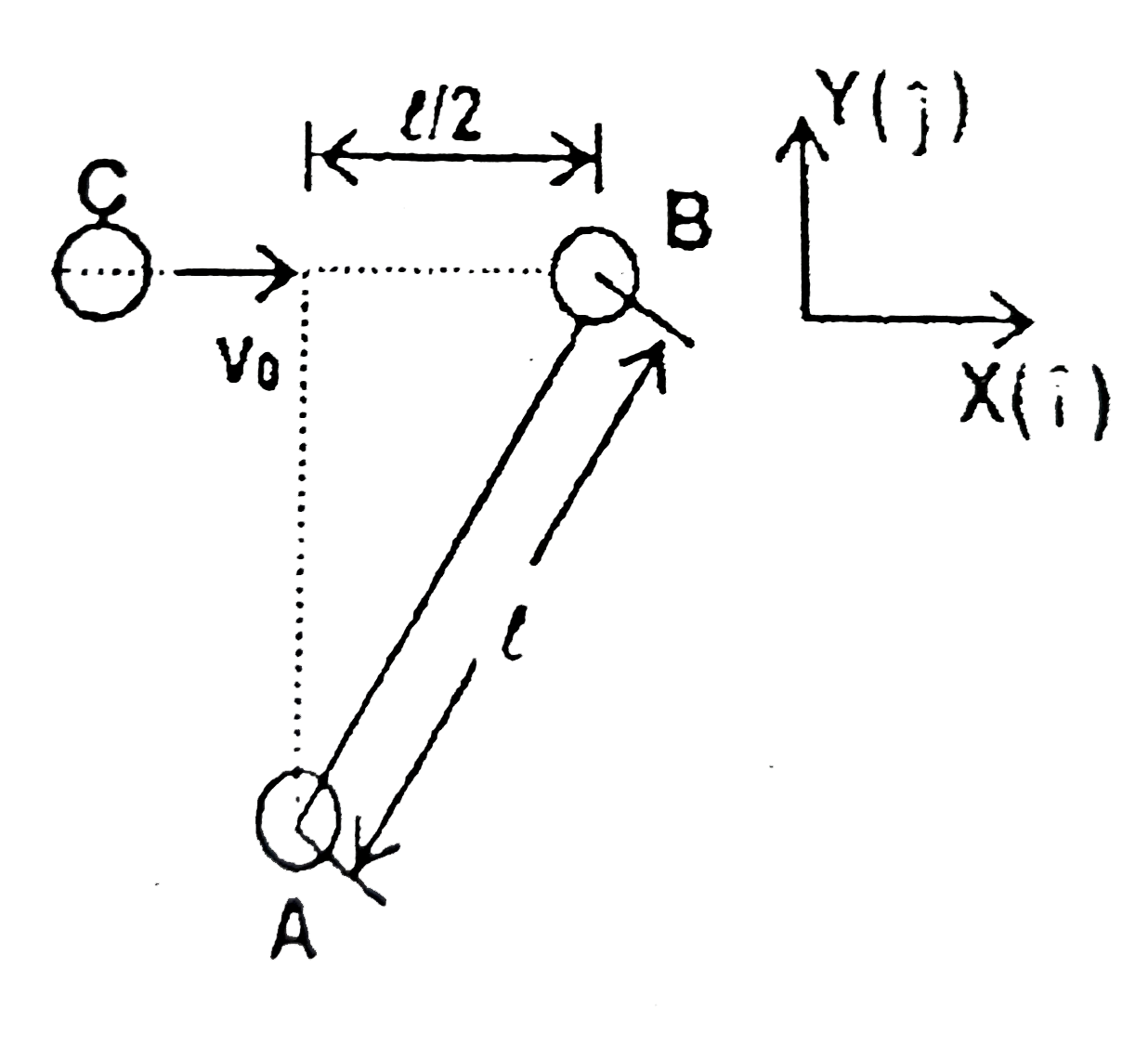 AˆiBˆi+ˆj√2C√32ˆi+12ˆjDCant't predict
AˆiBˆi+ˆj√2C√32ˆi+12ˆjDCant't predictThree spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming 'head on' inelastic impact between B and C, we cannot conserve kinetic energy of the entire system.

The magnitude of velocity of A immediately after collision isA√3v04Bv08Cv04D√mv08Three spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming 'head on' inelastic impact between B and C, we cannot conserve kinetic energy of the entire system.
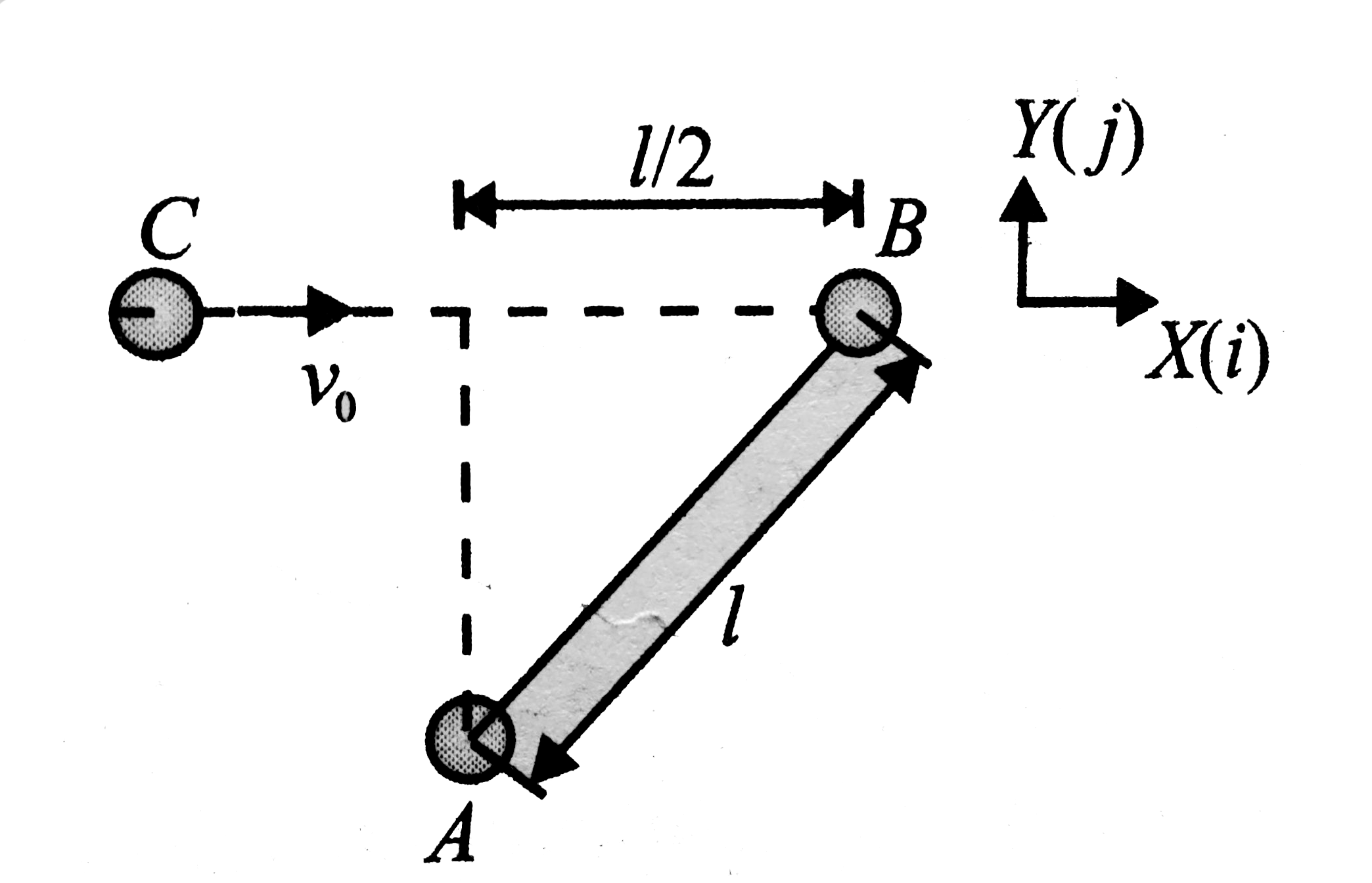 Velocity of A immediately after collision is along unit vector AˆjB12ˆi+√32ˆjCˆjDnone of these
Velocity of A immediately after collision is along unit vector AˆjB12ˆi+√32ˆjCˆjDnone of these
Three spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming 'head on' inelastic impact between B and C, we cannot conserve kinetic energy of the entire system.
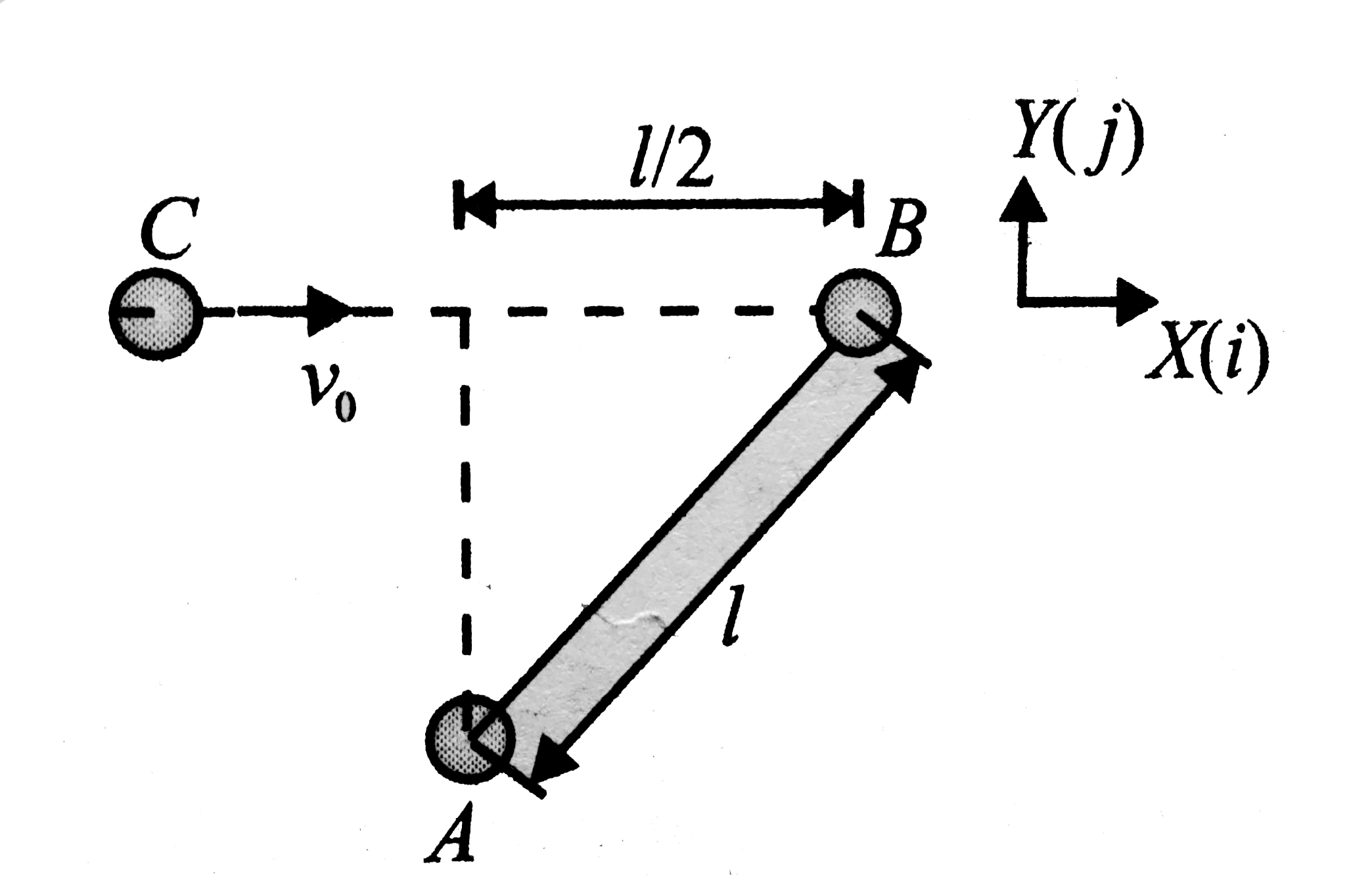 The velocity of B immediately after collision is along unit vector
The velocity of B immediately after collision is along unit vector
View SolutionThree spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming 'head on' inelastic impact between B and C, we cannot conserve kinetic energy of the entire system.
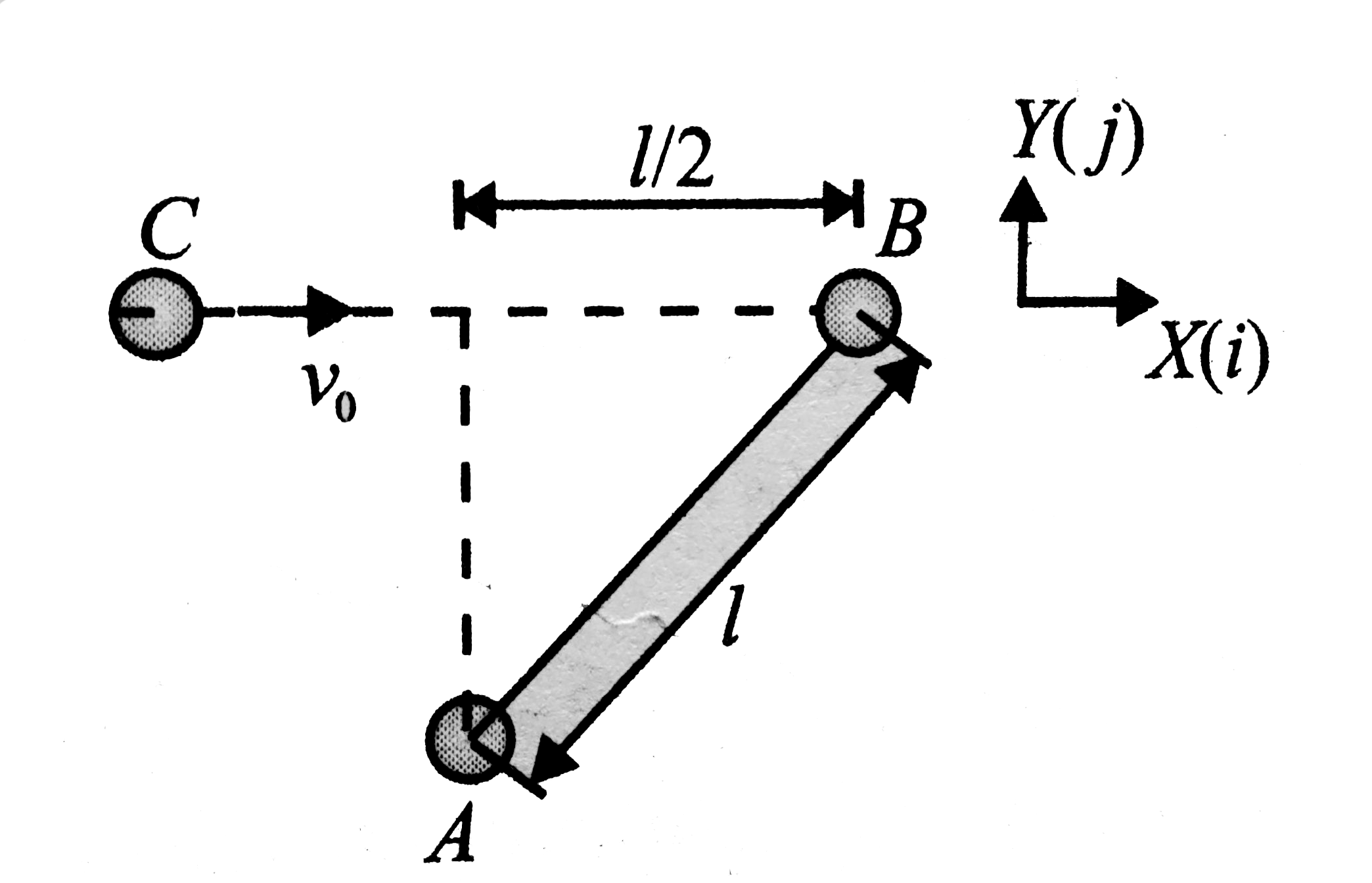
If velocity of C immediately after collision becomes v02 in the initial direction of motion, the impulse due to string on sphere A is
View SolutionThree spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming "Head on" inelastic impact between B and C, we can 't conserve kinetic energy of entire system.
If velocity of C immediately after collision becomes v02 in the initial direction of motion, the impulse due to string on sphere A is

View SolutionThree spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming 'head on' inelastic impact between B and C, we cannot conserve kinetic energy of the entire system.
 The velocity of B immediately after collision is along unit vector
The velocity of B immediately after collision is along unit vector
View SolutionThree spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming 'head on' inelastic impact between B and C, we cannot conserve kinetic energy of the entire system.

If velocity of C immediately after collision becomes v02 in the initial direction of motion, the impulse due to string on sphere A is
View Solution

