The area of the quadrilateral formed by the tangents from the point (4,5) to the circle x2+y2−4x−2y−11=0 with the pair of radii through the points of contact of the tangents is:
4 sq. units
8 sq.units
6 sq. units
none
The correct Answer is:B
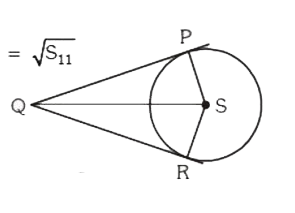
Center of tangent = √S11
∴QP=2
Radius =4
Area of PQRS = 2ΔPQRS
=4×2=8
Similar Questions
find the area of the quadrilateral formed by a pair of tangents from the point (4,5) to the circle x2+y2−4x−2y−11=0 and pair of its radii.
View SolutionIf the area of the quadrilateral formed by the tangent from the origin to the circle x2+y2+6x10y+c=0 and the pair of radii at the points of contact of these tangents to the circle is 8 sq. units, then c is a root of the equation
View Solution
Knowledge Check
If the area of a quadrilateral formed by the tangents from the origin to x2+y2+6x−10y+λ=0 and the pair of radii at the points of contact of these tangents to the circle, is 8 cm2, then the value of λ must be
A2B4C16D32A circle C1 of radius 2 units rolls o the outerside of the circle C2:x2+y2+4x=0 touching it externally.
Area of a quadrilateral found by a pair of tangents from a point of x2+y2+4x−12=0 to C2 with a pair of radii at the points of contact of the tangents is ( in sq. units )A2√3B4√3C√3D3√3The area of the triangle formed by the tangents from the point (4,3) to the circle x2+y2=9 and the line joining their points of contact in sq. units is
A13225B16225C19225Dnone
Find the area of the triangle formed by the tangents from the point (4, 3) to the circle x2+y2=9 and the line joining their points of contact.
View SolutionIf the area of the quadrilateral by the tangents from the origin to the circle x2+y2+6x−10y+c=0 and the radii corresponding to the points of contact is 15, then a value of c is 9 (b) 4 (c) 5 (d) 25
View SolutionThe angle between the pair of tangents from the point (1,12) to the circle x2+y2+4x+2y−4=0 is
View SolutionThe equation of pair of tangents drawn from the point (0,1) to the circle x2+y2–2x+4y=0 is–
View SolutionThe area of the quadrilateral formed by the tangents at the end points of latus rectum of the ellipse 5x2+9y2=45 is
View Solution

