Three resistances R1,R2andR3 are coonected in parallel . This combination is then connected to a celll of negligble internal resistance .Applying Kirchhoff's law prove that the equivalent resistance of the whole combination is give by ,
R=R1R2R3R1R2+R2R3+R1R3Solution in Bengali
Applying Kirchhoff's second law in the closed loop AR1BEA ,
i1R1−E=0
[ where emf of the cell is E and internal resistance is zero ]
∴i1=ER1 ....(1)
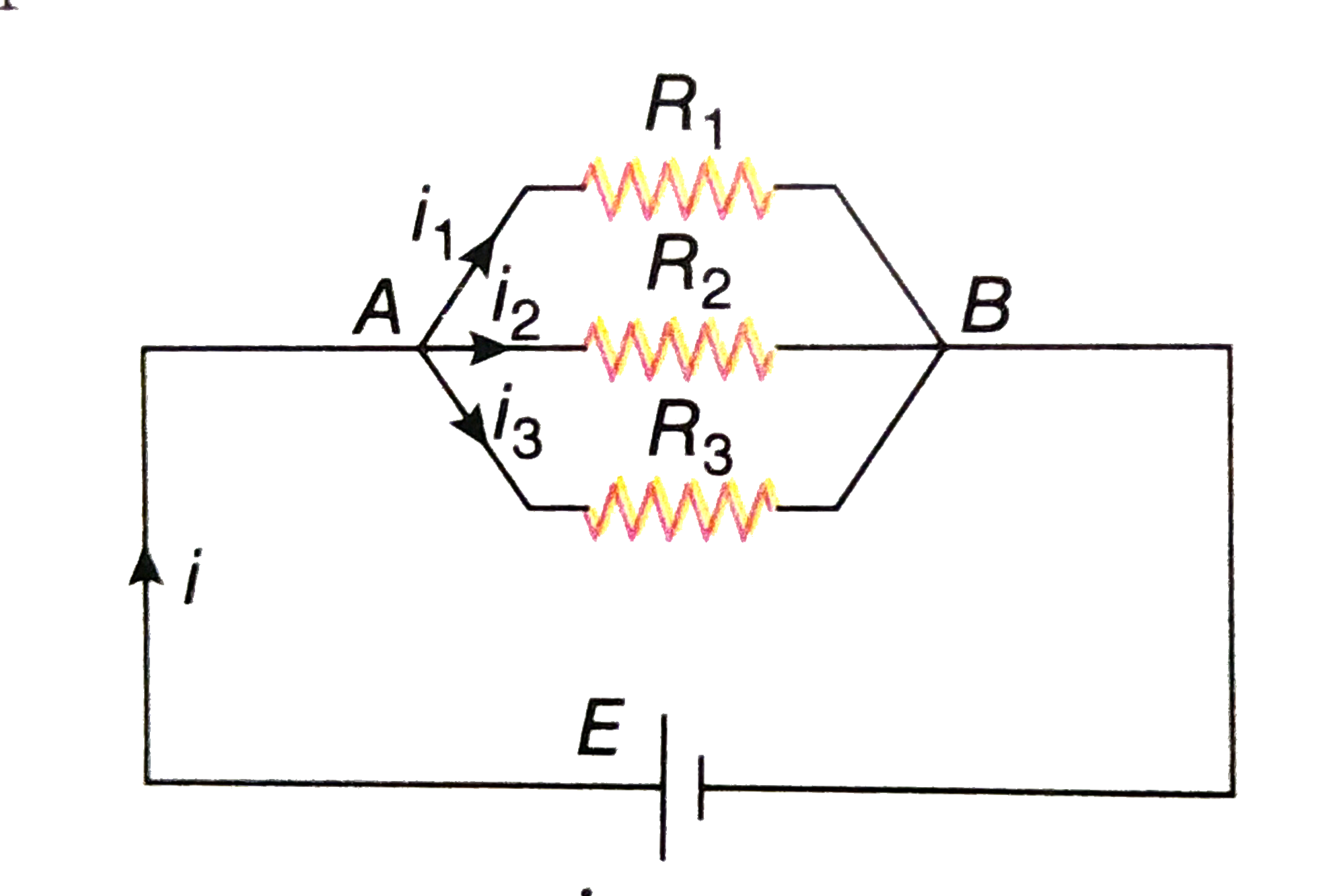
Again applying Kirchhoff's second law in AR2BEA ,
i2R2−E=0
∴i2=ER2 ....(2)
and similarly , i3=ER3 ...(3) ltbr gt From equatios (1) ,(2) and (3) we get ,
i1+i2+i3=E[1R1+1R2+1R3]=i[i=total current]
If R be the equivalent reistance then
R=Ei=11R1+1R2+1R3=R1R2R3R1R2+R2R3+R1R3
Similar Questions
Prove the questions
a(rr1+r2r3)=b(rr2+r3r1)=c(rr3+r1r2)
View SolutionTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View SolutionIn a ΔABC, if 2r2r3r2−r1=r3−r1 then
r1(r2+r3)√r1r2+r2r3+r3r1=
View SolutionFour resistors R_(1) , R_(2) , R_(3) and R_(4) are connected in parallel . The resultant resistance R is
View SolutionThe possible percentage error in computing the parallel resistance R of three resistances R1,R2,R3 from the formula 1R=1R1+1R2+1R3, if R1,R2,R3 are each 1.2% in error, is
View SolutionTwo resistors of resistances R_(1)=100 pm 3 ohm and R_(2)=200 pm 4 ohm are connected (a) in series, (b) in parallel. Find the equivalent resistance of the (a) series combination, (b) parallel combination. Use for (a) the relation R=R_(1)+R_(2) and for (b) 1/(R')=1/R_(1)+1/R_(2) and (Delta R')/R'^(2)=(Delta R_(1))/R_(1)^(2)+(Delta R_(2))/R_(2)^(2)
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View Solution
