The maximum energies of photoelectrons emitted by a metal are E1andE2 when the incident radiation has frequencies f1andf2 respectively. Show that Planck's constant h and the work function W0 of the metal are
h=E1−E2f1−f2,W0=E1f2−E2f1f1−f2Solution in Bengali
According to Einstein's photoelectric equation we have, E1=hf1−W0…(1)
E2=hf2−W0…(2)
E1−E2=h(f1−f2)
∴h=E1−E2f1−f2 [for E1>E2] ….(3)
Again multiplying equation (1) by f2 and equation (2) by f1 we obtain,
E1f2=hf1f2−f2W0...(4)
and E2f1=hf1f2−f1W0....(5)
Subtracting equation (5) from equation (4), we get
E1f2−E2f1=f1W0−f2W0=W0(f1−f2)
∴W0=E1f2−E2f1f1−f2
Similar Questions
माना कि S एक वृत्त है जो xy समतल में समीकरण x2+y2=4 के द्वारा परिभाषित है।
माना कि E1E2 और F1F2 वृत्त S की ऐसी जीवाएं हैं जो बिन्दु P0(1,1) से गुजरती हैं और क्रमश: x-अक्ष व y-अक्ष के समान्तर हैं। माना कि G1G2,S की वह जीवा है जो P0 से गुजरती है और जिसकी प्रवणता -1 है। माना कि E1 और E2 पर S की स्पर्शियां E3 पर मिलती हैं, F1 और F2 पर S की स्पर्शियां F3 पर मिलती हैं, तथा G1 और G2 पर S की स्पर्शियां G3 पर मिलती हैं। तब बिन्दु E3,F3 और G3 से गुजरने वाले वक्र का समीकरण है
View Solutionf1(x)=x+a,f2(x)=x2+bx+c and Δ=∣∣ ∣ ∣∣111f1(x1)f1(x2)f1(x3)f2(x1)f2(x2)f2(x3)∣∣ ∣ ∣∣, then Δ is independent of
View Solutionदो सदिशों F1 व F2 का परिमाण समान है जिसका मान F है। यदि |F1⋅F2|=|F1×F2| तब |F1+F2| बराबर है
View Solutionमाना कि S एक वृत्त है जो xy समतल में समीकरण x2+y2=4 के द्वारा परिभाषित है।
माना कि P वृत्त S पर स्थित एक ऐसा बिन्दु है जिसके दोनों निर्देशांक धनात्मक है। माना कि वृत्त S के बिन्दु P पर स्पर्शी निर्देशांक अक्षों को बिन्दुओं M और N पर प्रतिच्छेद करती है। तब रेखाखण्ड MN के मध्य बिन्दु से गुजरने वाले वक्र का समीकरण है
View Solutionमाना कि S एक वृत्त है जो xy समतल में समीकरण x2+y2=4 के द्वारा परिभाषित है।
माना कि E1E2 और F1F2 वृत्त S की ऐसी जीवाएं हैं जो बिन्दु P0(1,1) से गुजरती हैं और क्रमश: x-अक्ष व y-अक्ष के समान्तर हैं। माना कि G1G2,S की वह जीवा है जो P0 से गुजरती है और जिसकी प्रवणता -1 है। माना कि E1 और E2 पर S की स्पर्शियां E3 पर मिलती हैं, F1 और F2 पर S की स्पर्शियां F3 पर मिलती हैं, तथा G1 और G2 पर S की स्पर्शियां G3 पर मिलती हैं। तब बिन्दु E3,F3 और G3 से गुजरने वाले वक्र का समीकरण है
View SolutionFor the following table, the values of f1, f0 and f2 are respectively______.
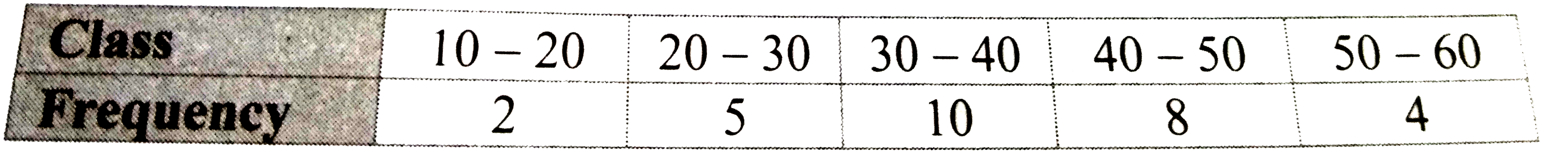
View SolutionFor x∈R,x≠0,x≠1, let f0(x)=11−x and fn+1(x)=f0(fn(x)),n=0,1,2,.... Then the value of f100(3)+f1(23)+f2(32) is equal to
View SolutionIf F_(1) and F_(2) are two vectors of equal magnitudes F such that |F_(1).F_(2)|= |F_(1)xxF_(2)|, "then"|F_(1) +F_(2)| equals to
View Solution
