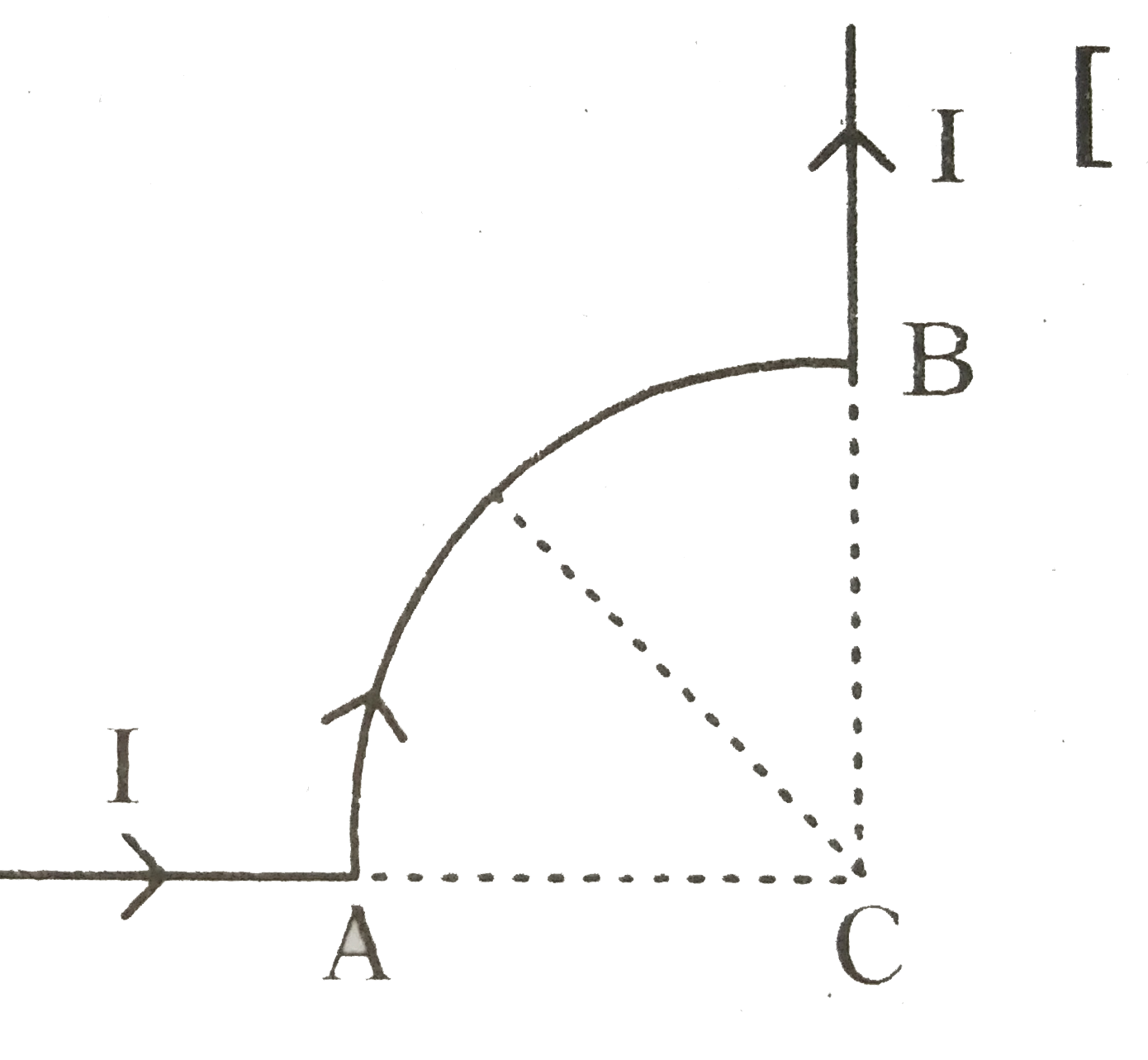
A wire carrying current I is shaped as shown in the figure. The section AB is quarter circle of radius r. The magnetic field is directed .
 Solution in Telugu
Solution in Telugu
At any angle π/4 to the plane of the paper.
Along the bisector of the angle ACB towards AB .
Along the bisector of the angle ACB away from AB.
Perpendicular to the plane of paper in downward direction.
The correct Answer is:D
we know that as the current in the loop flows in clockwise direction, therefore magnetic field due to current at the centre of the loop will be perpendicular to the plane of the paper in the downward direction .
Similar Questions
एक लम्बे तार को, जिसमें i धारा प्रवाहित हो रही है, चित्रानुसार मोड़ा गया है। चाप AB त्रिज्या r के वृत्त का एक-चौथाई भाग है। केन्द्र C पर चुम्बकीय क्षेत्र की दिशा है
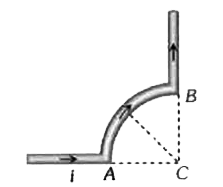
View SolutionA rigid wire consists of a semicircular portion of radius R and two straight sections the wire is partially immersed in a perpendicualr magnetic field B as shown in the figure. Find the magnetic force on the wire if it carries a current i.
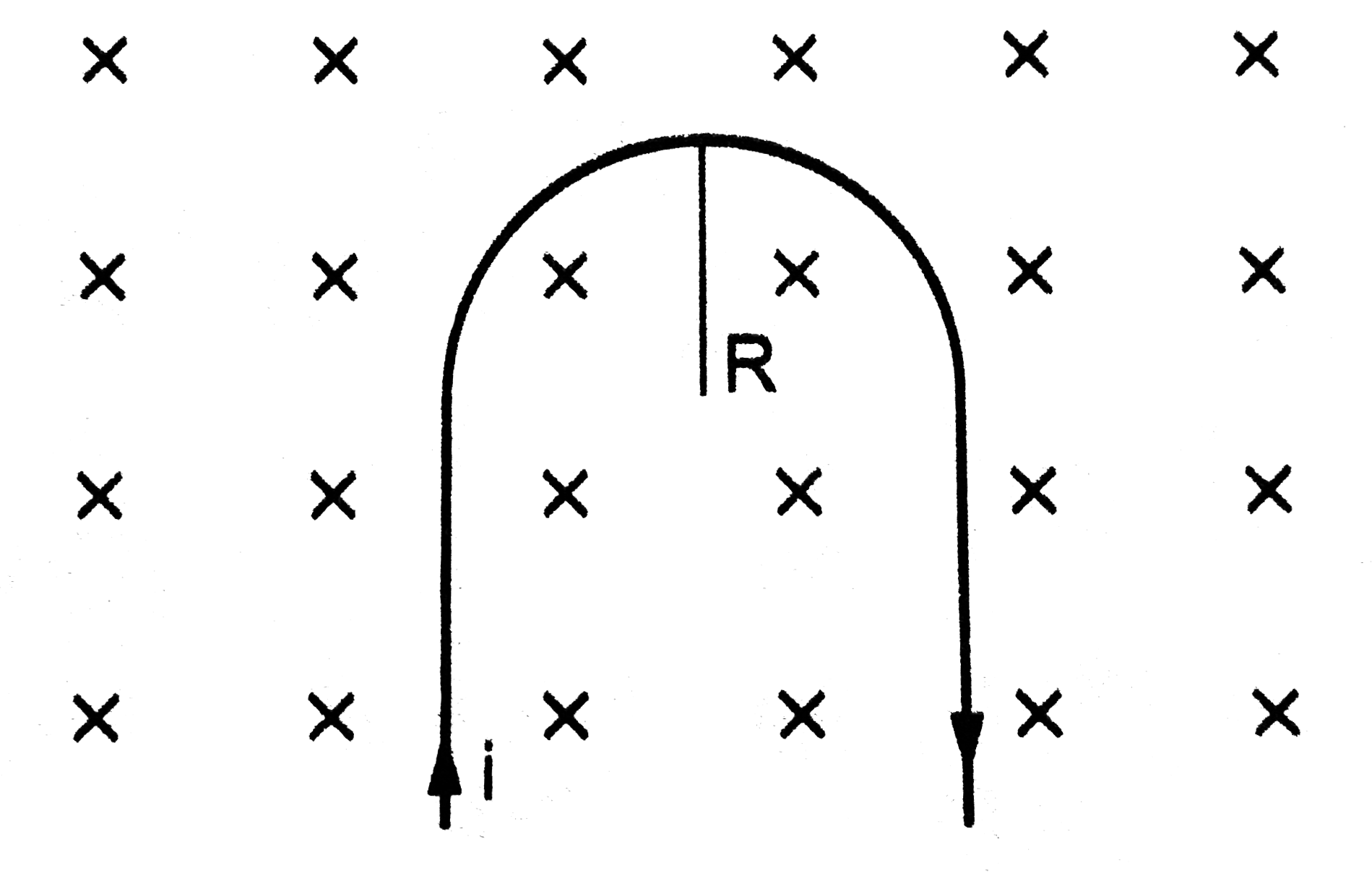
View SolutionIn the following figure , magnetic field of different current - carrying wires is shown . Which figure represents the correct direction of the magnetic field ?
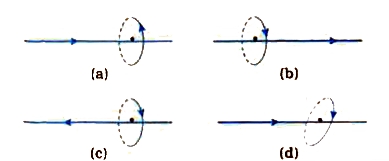
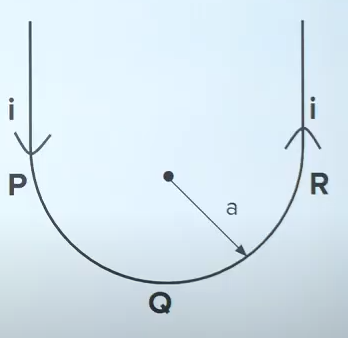
View SolutionIn figure shown U-shaped wire a current i is flowing as shown. Section PQR is a semicircle of radius a.If O is origin then find magnetic field at O
View SolutionAn infinite straight current carrying conductor is bent into a circle as shown in the figure
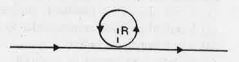 . If the radius of the circle is R, the magnetic field at the centre of the coil is :
. If the radius of the circle is R, the magnetic field at the centre of the coil is :
View SolutionA wire carrying current i is shaped as shown
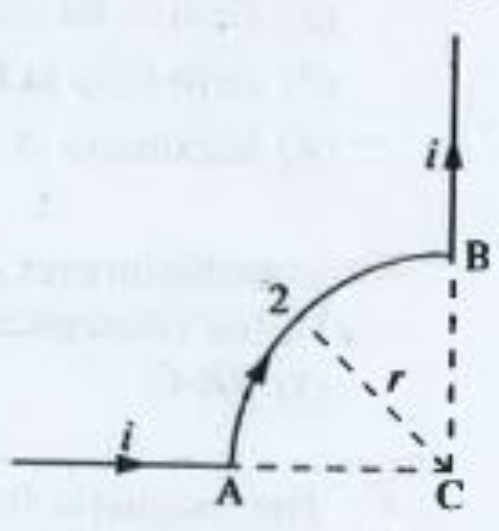 . Section AB is a quarter circle of radius r. The magnetic field is directed
. Section AB is a quarter circle of radius r. The magnetic field is directed
View SolutionThe wire shown in Fig. carries current I in the direction shown. The wire consists of a very long, straight section, a quarter- circle with radius R, and another long, straight section. What are magnitude and direction of net magnetic field at the center of curvature of quarter-circle section (point P)?

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
View Solution
