A circular metallic ring of radius R has a small gap of width d. The coefficient of thermal expansion of the metal is α in appropriate units. If we increase the temperature of the ring by a amount ΔT, then width of the gap – (A) Will increases by an amount dαΔT
Will increases by an amount dαΔT
will not change
Will increases by an amjoint (2πR−d)αΔT
Will decreases by an amount dαΔT
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
The radius of a ring is R and its coefficient of linear expansion is α. If the temperature of ring increases by θ then its circumfrence will increase by
View SolutionA piece of metal floats on mercury. The coefficients of volume expansion of the metal and mercury are γ1 and γ2 respectively. If the temperatures of both mercury and the metal are increased by an amount ΔT, the fraction of the volume of the metal submerged in mercury changes by the factor............
View Solution
Knowledge Check
The diameter of a metal ring is D and the coefficient of linear expansion is α. If the temperature of the ring is increased by 10C, the circumference and the area of the ring will increases by
AπDα,2πDαB2πDα,πD2αCπDα,πDα2DπDα,πD2α2The radius of a ring is R and its coefficient of linear expansion is α. If the temperature of ring increases by θ then its circumfrence will increase by
AπRαθB2πRαθCπRαθ2DπRαθ4The radius of metal sphere at room temperature T is R and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature T, so that new temperature is T+ΔT. The increase in volume of sphere is approximately
A2πRαΔTBπR2αΔTC4πR3αΔT3D4πR2αΔT
The radius of a metal sphere at room temperature T is R, and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature ΔT so that its new temperature is T+ΔT. The increase in the volume of the sphere is approximately
View SolutionA circular metallic ring has a radius r. A battery of V volts is connected across the diameter of the ring as shown in the adjoining figure. Calculate the magnetic field at the centre of the coil.
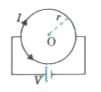
View SolutionThe radius of metal sphere at room temperature T is R and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature T, so that new temperature is T+ΔT. The increase in volume of sphere is approximately
View SolutionThe diameter of a fly wheel is R. Its coefficient of linear expansion is α. If its temperature is increased by δT the percentage increase in its moment of inertia is
View SolutionThe radious of a metal sphere at room temperature T is R, and the coefficient of linar expansion of the metal is α. The sphere is heated a little by a temperature ΔT so that its new temperature is T+ΔT. The increase in the volume of the sphere is approximately
View Solution

