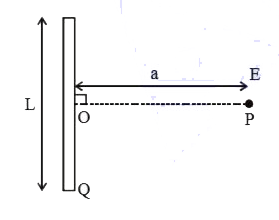
Calculate the potential due to a thin uniformly charged rod of length L at the poiot P shown in figure. The lioear charge density of the rod is λC/m

Step by step video & image solution for Calculate the potential due to a thin uniformly charged rod of length L at the poiot P shown in figure. The lioear charge density of the rod is lambda C//m by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The electrostatic potential due to the charge configuration at point P as shown in figure for bltlta is
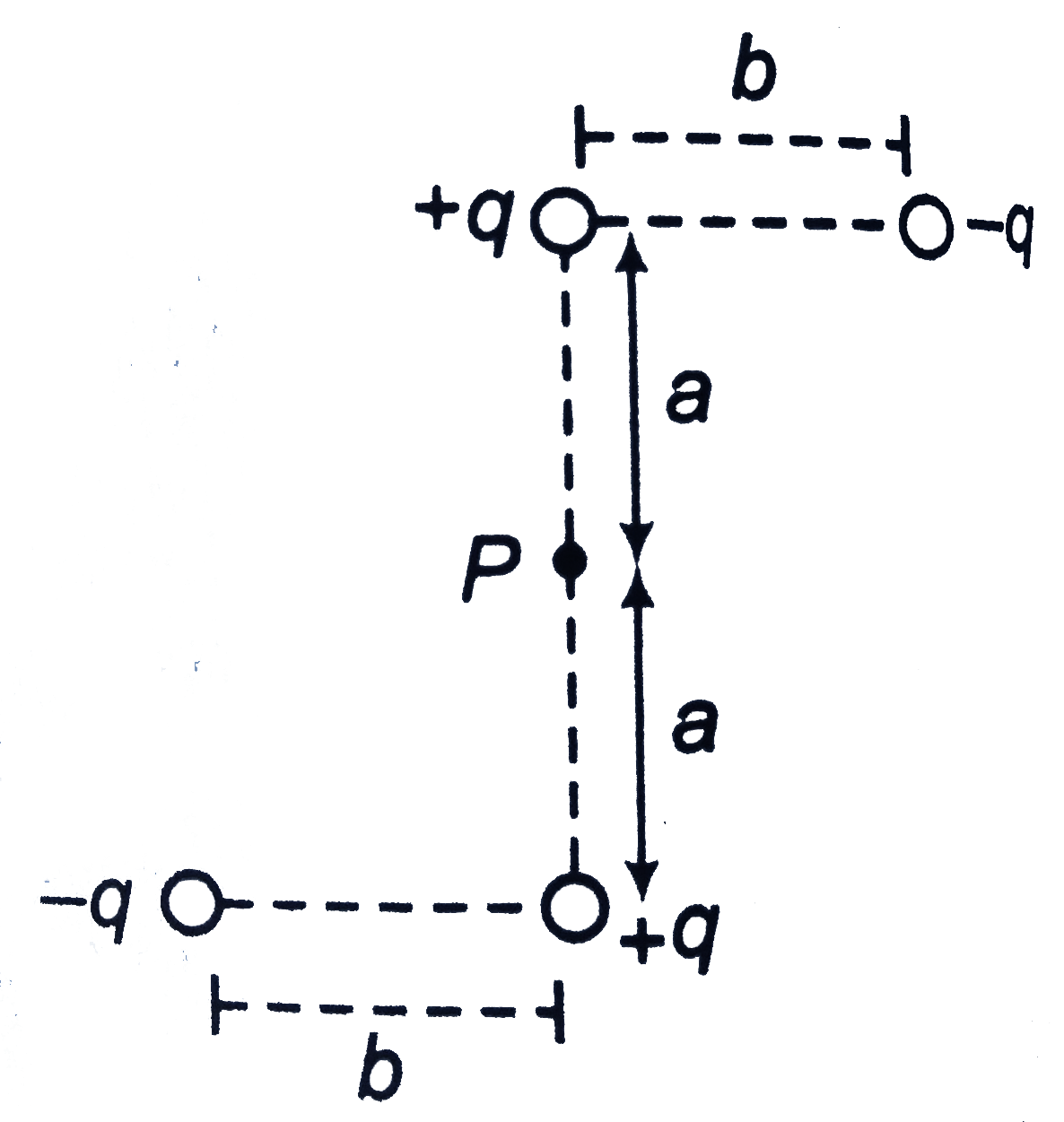 A2q4πε0aB2qb24πε0a3Cqb24πε0a3Dzero
A2q4πε0aB2qb24πε0a3Cqb24πε0a3DzeroIf linear charge density of a wire as shown in the figure is λ
 Apotential at the centre is λ2ε0Belectric field at the centre of the loop is λ2πε0RCelectric field at the centre of the loop is λ2πε0R+λ2ε0RDNone of the above
Apotential at the centre is λ2ε0Belectric field at the centre of the loop is λ2πε0RCelectric field at the centre of the loop is λ2πε0R+λ2ε0RDNone of the aboveFind the electric field at point P (as shown in figure) on the perpendicular bisector of a uniformly charged thin wire of length L carrying a charge Q. The distance of the point P from the centre of the rod is a =√32L.
 A√3Q4πε0L2BQ3πε0L2CQ2√3πε0L2DQ4πε0L2
A√3Q4πε0L2BQ3πε0L2CQ2√3πε0L2DQ4πε0L2
Calculate electric field intensity at point P due to a thin positive uniformly charged rod . Point P is at perpendicular distance d from the rod . The lower and upper ends of the rod make the angles α and β as shown below .
View SolutionFind the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The lengthof the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionA positively charged rod lies along X-axis in such a manner that one end of the rod is at the origin and the other end at x=−∞. The linear charge density for the rod is λ. Electric field intensity at x =a is
View SolutionCharge Q is uniformly distributed on a dielectric rod AB of length 2l. The potential at P shown in the figure is equal to

View Solution


