If you want to pile up sand onto a circular area of radius R. The greatest height of the sand pile that can be created without spilling the sand onto the surrounding. Area, if μ is the coefficient of friction between sand particle is:
μ2R
μR
R
Rμ
The correct Answer is:b
Similar Questions
A worker wishes to pile a cone of sand onto a circular area in his yard. The radius of the circle is r,and no sand is to spill on to the surrounding area. If μ is the static coefficient of friction between each layer of sand along the slope and the sand, show that the greatest volume of sand that can be stored in this manner is 13πμR3.
View SolutionA worker wishes to pile up sand on to a circular area of radius R. No sand is to spill on to the surrounding area. If μs is the coefficient of static friction of sand on sand,the sand pile . Density of sand =ρ
View Solution
Knowledge Check
The greatest height h of the sand pile that can be erected without spilling the sand onto the surrounding circular area of radius R (If μ is the coefficient of friction between sand particles) is
ARBRμCμRDμ2RA worker wishes to pile up sand on to a circular area of radius R. No sand is to spill on to the surrounding area. If μs is the coefficient of static friction sand particles, then choose the correct statement (s)
AThe greatest height of sand pile that can be created is μsR.BThe greatest height of sand pile that can be created is R/μsCMinimum work required to create greatest height sand pile is π12μ2sR4ρg. Where ρ is the density of sand volumeDSand pile will be in stable equilibriumThe maximum speed that can be achieved without skidding by a car on a circular unbanked road of radius R and coefficient of static friction μ , is
AμRgBRg√μCμ√RgD√μRg
A car is moving along a banked road laid out as a circle of radius r . (a) What should be the banking angle θ so that the car travelling at speed v needs no frictional force from tyres to negotiate the turn ? (b) The coefficient of friction between tyres and road are μs=0.9 and μk=0.8 . At what maximum speed can a car enter the curve without sliding toward the top edge of the banked turn ?

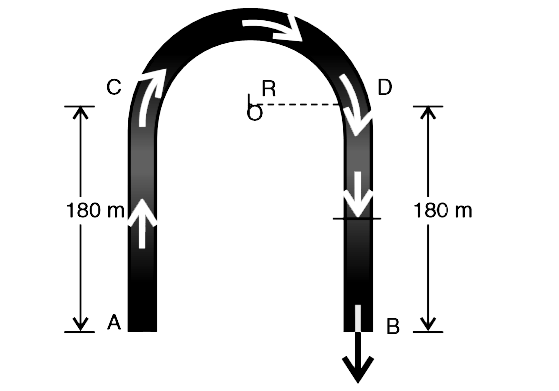
View SolutionA flat race track consists of two straight section AC and DB each of length 180 m and one semi circular section DC of radius R = 150 m. A car starting from rest at A has to reach B in least possible time (the car may cross through point B and need not stop there). The coefficient of friction between the tyres and the road is μ=0.6 and the top speed that the car can acquire is 180 kph. Find the minimum time needed to move from A to B under ideal conditions. Braking is not allowed in the entire journey [g=10m/s2]
View SolutionAn inclined plane of angule a is fixed onto a horizontal turntable with its line of greater slope in same plane as a diameter of forntable .A small block is placed on the inclined plane a distance r from the axis the coefficient of fraction between the block and the inclined plane is μ The turntable along with incline plane spins about its axis with constant minimum angular velocity ω
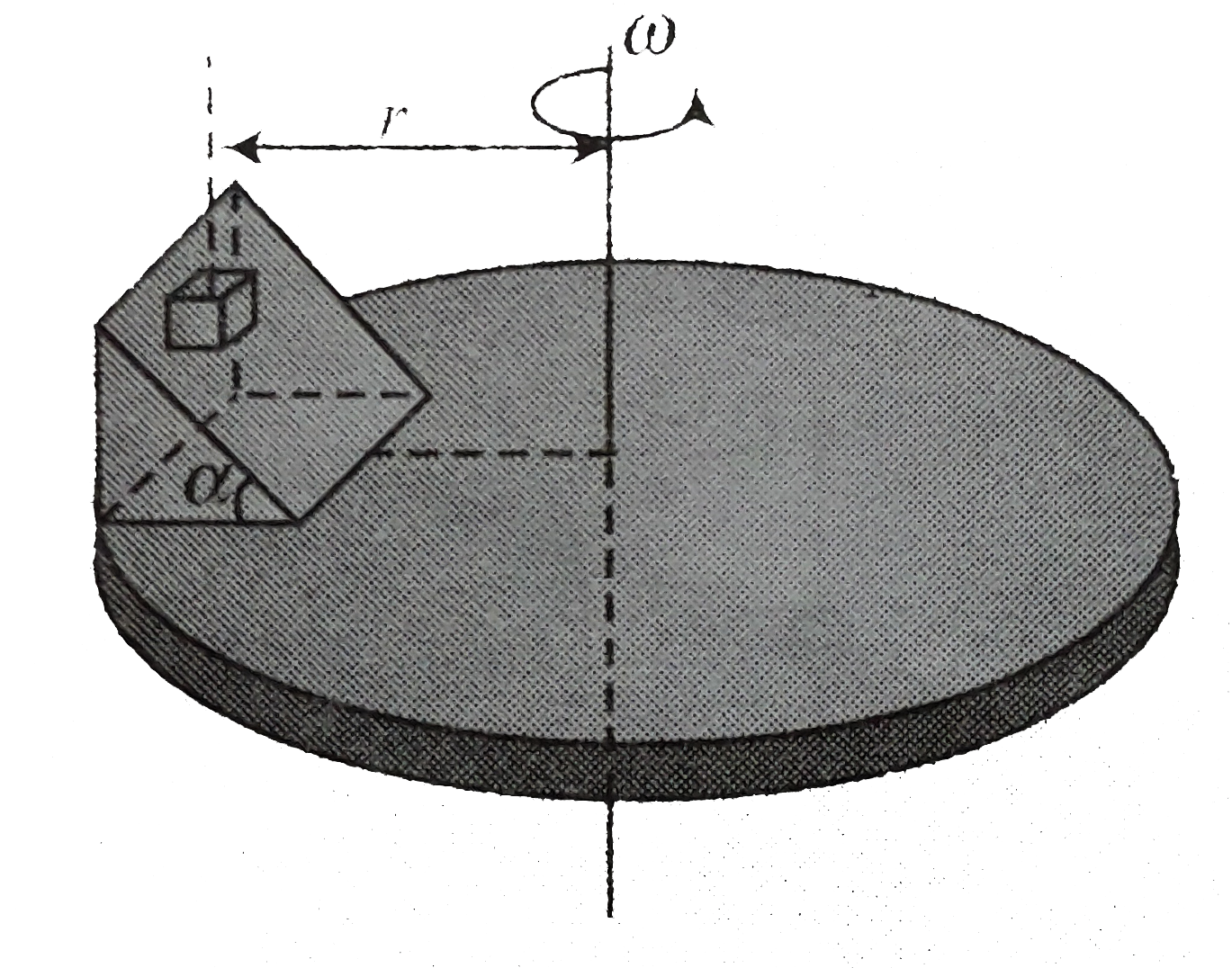
a. Find an capression for the minimum angular velocity ω to prevent the block from sliding down the plane in term of g,r,μ and the plane ω
b. Now a block of mass but having coefficient friction (with inclined plane)2μ is kept instead of the original block . find the radius of friction force acting between block and incline now to the friction force active in part (a)
View SolutionA house is built on the top of a hill with 45∘slope Due to the sliding of meterial and sand top from top to the bottom of till , the slip angle has been redaced if the coefficient of static friction between sand particles is 0.75 what is the final angle attated by bill ? (tan−10.75=37∘)

View SolutionA sack of sand is lying on a light carpet on a horizontall surface. With the help of the carpet the sack of mass M is to be pulled from one rough surface to other rough surface of same length. How much work is done if the coefficient of kinetic friction between the surfaces and the carpet are μ1 and μ2 ? The weight of the sack is not uniform, but we know that the centre of mass of the sack is at a distance of s1, and s2 from the ends of the bag. [Length of both surfaces is s1+s2. Initially sack completely covers left surface and finally the sack completely covers the right surface] (assume that the sack does not deform)
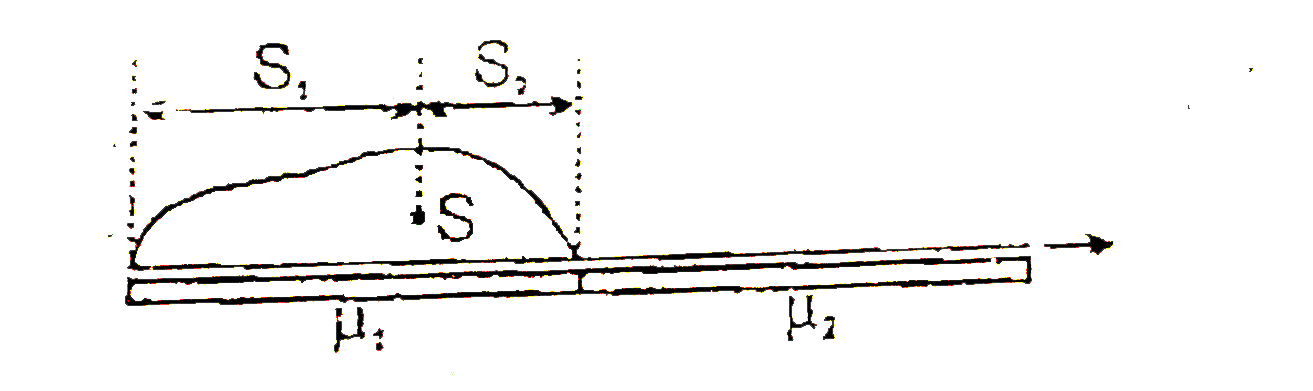
View Solution

