A single conservative f(x) acts on a m=1kg particle moving along the x-axis. The potential energy U(x) is given by :
U(x)=20+(x−2)2
where x is in metres. At x=5m, a particle has kintetic energy of 20 J
The minimum speed of the particle is:
1m/s
√40m/s
√58m/s
zero
The correct Answer is:D
Step by step video, text & image solution for A single conservative f_((x)) acts on a m = 1 kg particle moving along the x-axis. The potential energy U_((x)) is given by : U_((x)) = 20 + (x - 2)^(2) where x is in metres. At x = 5 m, a particle has kintetic energy of 20 J The minimum speed of the particle is: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Match the following :
Column-I Column-II(A)Work done by all the forces(P)Change in potential energy(B)Work done by conservative forces(Q) Change in kinetic energy(C)Work done by external forces(R) Change in mechanical energy(S) None
View SolutionThe potential energy U in joule of a particle of mass 1kg moving in x−y plane obeys the lawU=3x+4y, where (x,y) are the co-ordinates of the particle in metre. If the particle is at rest at (6,4) at time t=0 then :
View SolutionMatch the column :
Column-I (Quantity)Column-II(Unit)(a)Energy density (Energy per unit volume)(p)dyne/cm2(b)Force constant of a spring(r)kg−m/s(c)Pressure(r)erg/cm2(s)pascal
View SolutionA single conservative fore F_(x) acts on a 2kg particle that moves along the x-axis. The potential energy is given by. U =(x-4)^(2)-16 Here, x is in metre and U in joule. At x =6.0 m kinetic energy of particle is 8 J find . (a) total mechanical energy (b) maximum kinetic energy (c) values of x between which particle moves (d) the equation of F_(x) as a funcation is zero (e) the value of x at which F_(x) is zero .
View SolutionA single conservative force F(x) acts on a 1.0-kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x-2)^2 where x is in meters. At x=5.0m , the particle has a kinetic energy of 20J . What is the mechanical energy of a system?
View SolutionA single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
The maximum and minimum values of x, respectively, are
View SolutionA single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
Determine the equation of F(x) as a function of x.
View SolutionA partical of mass 2kg is moving on the x- axis with a constant mechanical energy 20 J . Its potential energy at any x is U=(16-x^(2))J where x is in metre. The minimum velocity of particle is :-
View SolutionA single conservative f_((x)) acts on a m = 1 kg particle moving along the x-axis. The potential energy U_((x)) is given by : U_((x)) = 20 + (x - 2)^(2) where x is in metres. At x = 5 m , a particle has kintetic energy of 20 J The maximum speed of the particle is:
View SolutionA single conservative f(x) acts on a m=1kg particle moving along the x-axis. The potential energy U(x) is given by :
U(x)=20+(x−2)2
where x is in metres. At x=5m, a particle has kintetic energy of 20 J
The maximum value of potential energy is:
View SolutionA single conservative f_((x)) acts on a m = 1 kg particle moving along the x-axis. The potential energy U_((x)) is given by : U_((x)) = 20 + (x - 2)^(2) where x is in metres. At x = 5 m , a particle has kintetic energy of 20 J The least value of x (position of particle is ) will be:
View SolutionA single conservative f_((x)) acts on a m = 1 kg particle moving along the x-axis. The potential energy U_((x)) is given by : U_((x)) = 20 + (x - 2)^(2) where x is in metres. At x = 5 m , a particle has kintetic energy of 20 J The largest value of x will be:
View SolutionA single conservative f(x) acts on a m=1kg particle moving along the x-axis. The potential energy U(x) is given by :
U(x)=20+(x−2)2
where x is in metres. At x=5m, a particle has kintetic energy of 20 J
The position of equilibrium and its nature is:
View SolutionA single conservative force F(x) acts on a particle that moves along the x - axis. The graph of the potential energy with x is given. At x=5m, the particle has a kinetic energy of 50 J and its potential energy is related to position 'x' as U=15+(x−3)2 Joule where x is in meter. Then:
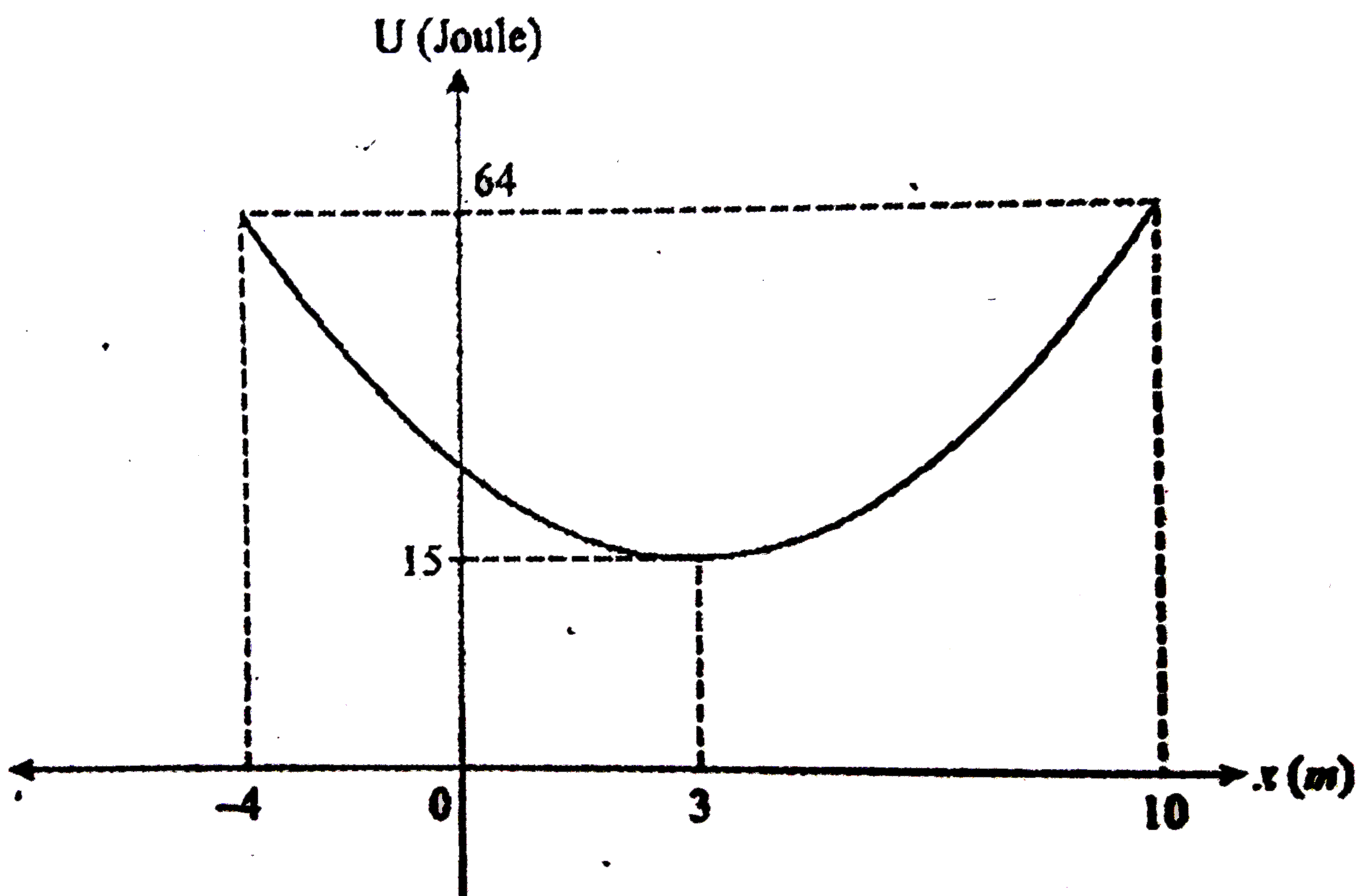
View SolutionA single conservative force F(x) acts on particle that moves along the x-axis. The graph of the potential energy with x is given. At x = 5m , the particle has a kinetic energyof 50 J and its potential energy is related to position 'x' as U = 15 + (x - 3)^(2) Joule, where x is in mete then :
View Solution

