Two electric dipoles , each of dipole moment p=6.2×10−30 C m are placed with their axes along the same line their centre a distance d=10−8 m apart . Calculate the force of attraction between the dipoles .
The correct Answer is:2.1×10−16N
Step by step video, text & image solution for Two electric dipoles , each of dipole moment p = 6.2 xx 10^(-30) C m are placed with their axes along the same line their centre a distance d = 10^(-8) m apart . Calculate the force of attraction between the dipoles . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A proton is placed at a distance of 3 xx 10^(-9) m from the centre of an electric dipole along the axis of the dipole. Calculate the force on the proton due to dipole if its dipole moment is 4 xx 10^(-30) C m. Given: Dipole length < < 3xx10^(-9) m.
View SolutionAn electric dipole with dipole moment 4×10−9 c m is aligned at 30∘ with the direction of a uniform electric field of magnitude 5×104NC−1. calculate the magnitude of the torque acting on the dipole
View SolutionAn electric dipole with dipole moment 4×10−9 c m is aligned at 30∘ calculate the magnitude of the torque acting on the dipole
View SolutionTwo electric dipoles each of dipole moment P=6.2×10−30C−m are placed with their axis along the same line and their centres at a distanced = 10−8cm. The force of attraction between dipoles is
View SolutionAn electric dipole, when held at 30^(@) with respect to a uniform electric field of 10^(4) N //C experiences a torqueof 9 xx 10^(-26) N m . Calculate dipole moment of the dipole.
View SolutionThe electric potential at a distance of 3 m on the axis of a short dipole of dipole moment 4×10−12 coulomb-metre is
View SolutionTwo identical electric dipoles of dipole moments p are placed as shown in the figure. The electrostatic force on dipole placed along x-axis is (d << r) (14πε0 )
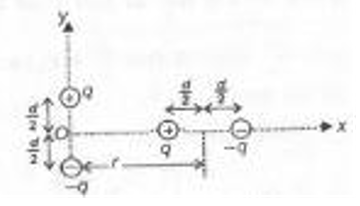
View SolutionFind the force of interaction of two dipoles , if the two dipole moments are parallel to each other and placed at a distance x apart
View Solution
