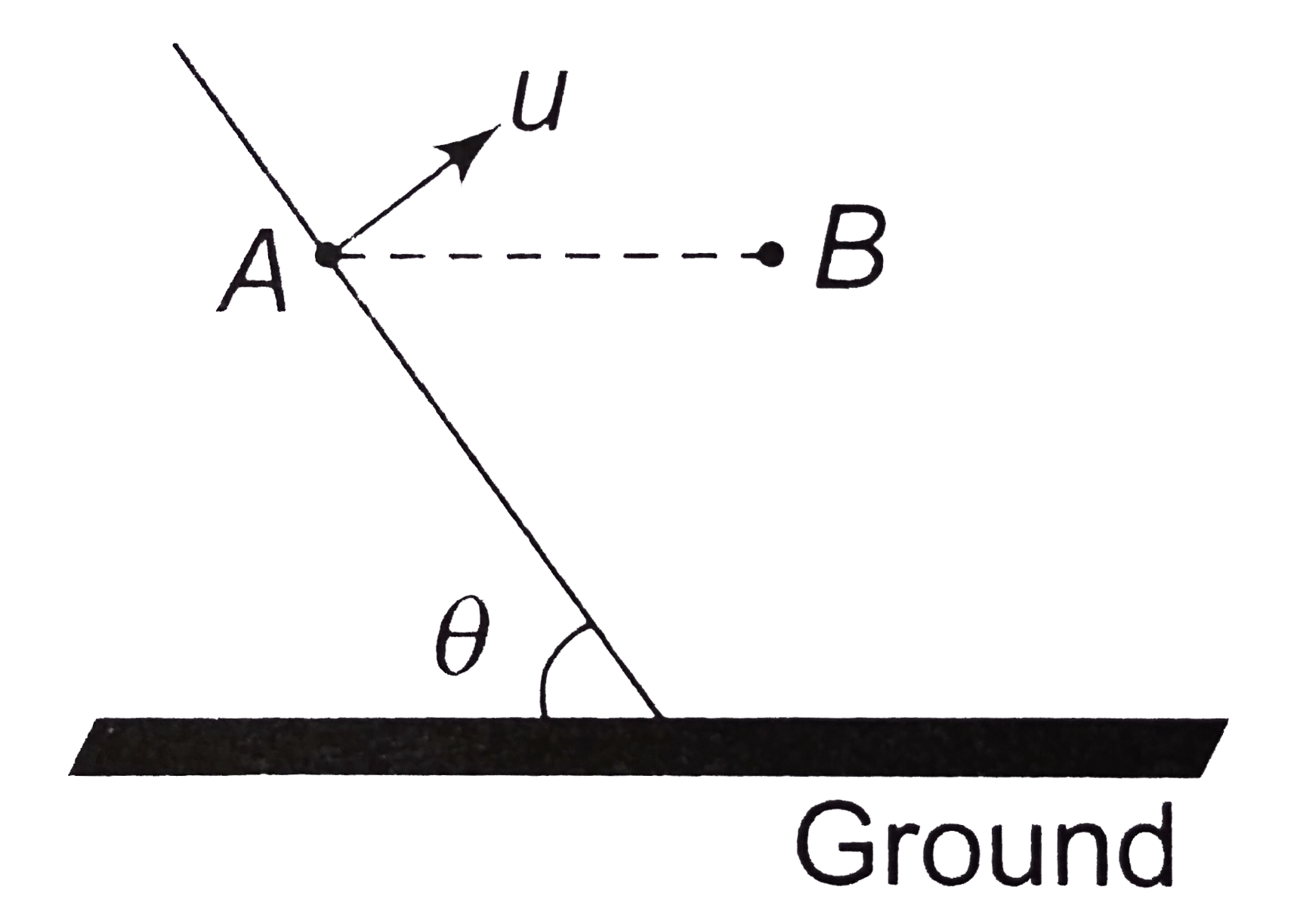
A particle is projected at point A from an inclination plane with inclination angle θ as shown in figure. The magnitude of projection velocity is →u and its direction is perpendicular to the plane. After some time it passes from point B which is in the same horizontal level of A, with velocity →v. Then the angle between →uand→v will be
The correct Answer is:⎡⎢⎣u=[gR(1+3sin2β)2sinβ]1/2⎤⎥⎦
Step by step video, text & image solution for A particle is projected at point A from an inclination plane with inclination angle theta as shown in figure. The magnitude of projection velocity is vecu and its direction is perpendicular to the plane. After some time it passes from point B which is in the same horizontal level of A, with velocity vecv. Then the angle between vecu and vecv will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
At what distance from the center of the earth will a 1 kg object have a weight of 1N ? If released from rest at this distance, What will its initial acceleration be ?
View SolutionA particle is projected horizontally with a speed ''u'' rom the top of plane incline at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?
View SolutionLet →u,→vand→w be such that |→u|=1,|→v|=2and|→w|=3 if the projection of →v along →u is equal to that of →w along →u and vectors →vand→w are perpendicular to each other then |→u−→v+→w| equals
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontally with a speed "u" from the top of plane incline at an angle ..θ.. with the horizontal. How far from the point of projection will the particle strike the plane ?
View SolutionA particle is projected horizontally with a speed "u" from the top of plane incline at an angle ..θ.. with the horizontal. How far from the point of projection will the particle strike the plane ?
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will particle strike the plane?
View SolutionA particle is projected horizontally with a speed "u" from the top of plane incline at an angle "θ" with the horizontal. How far from the point of projection will the particle strike the plane?
View Solution

