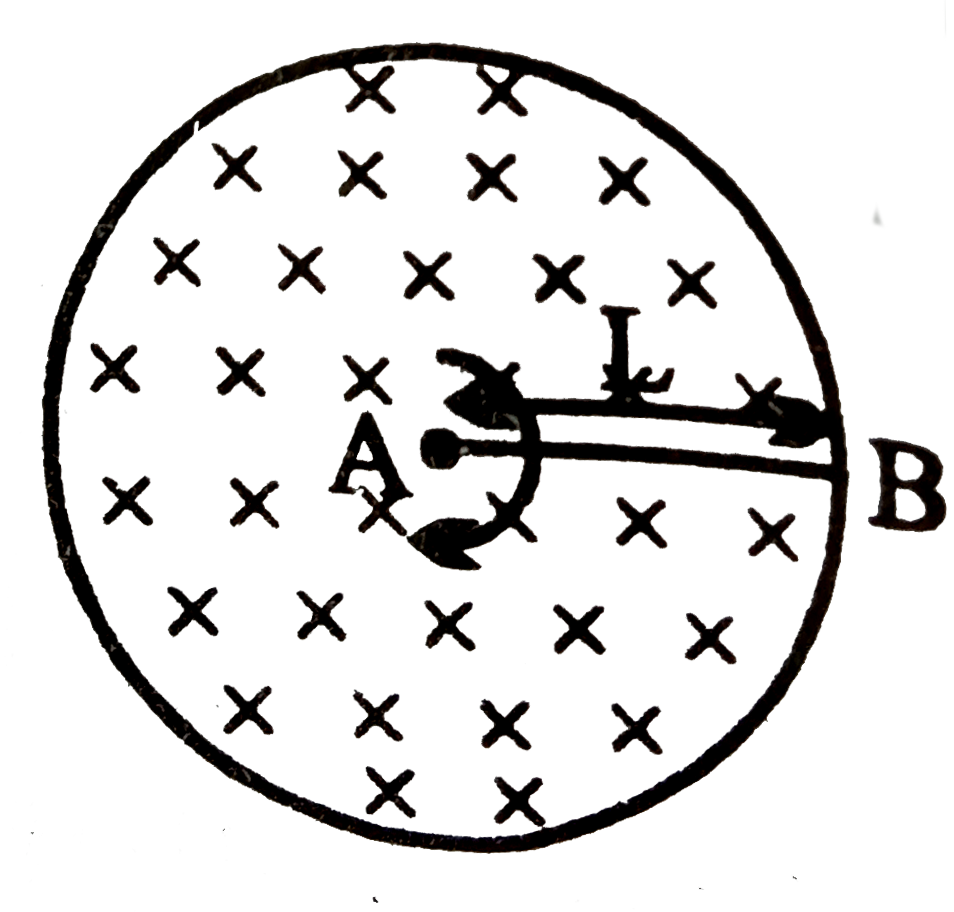
A copper rod AB of length l is rotated about one end A with a constant angular velocity ω. Calculate the electric field at a distance x from the axis of rotation. Also determine PD between A and B.
The correct Answer is:mw2xe,12mw2l2e
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENIALBOOK - NN GHOSHCHAPTER - ELECTRIC FIELD AND POTENIALEXERCISE - EXERCISE
21 Videos
- DYNAMO, MOTOR, TRANSFORMERBOOK - NN GHOSHCHAPTER - DYNAMO, MOTOR, TRANSFORMEREXERCISE - EXERCISE
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NN GHOSHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERICISES-B
18 Videos
Similar Questions
The force of attraction between two charges +30×10−9Cand−20×10−9C seperated by a distance of 020m is found to be 5 xx 10^(-5)N. Find the relative permittivity of the medium.
View SolutionThe equation of an alternating currect is i=2sin200πt. Calculate (i) the prak volue of the currect (ii) the mean volue of the currect (iii) virtual current.
View SolutionHalf of the core of a solenoid of 2×10−3m2 cross -section , is made up of air and the other half iron (μr=500). The length of the solenoid is 2 m . If the number of turns is 1000, calculate its coefficient of self induction .
View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA copper rod AB of length L, pivoted at one end A, rotates at constant angular velocity omega, at right angles to a uniform magnetic field of induction B. The e.m.f developed between the mid point C of the rod and B is
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
View SolutionWhen a rod of length l is rotated with angular velocity of ω in a perpendicular field of induction B , about one end , the emf across its ends is
View SolutionA copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity omega about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA copper rod of length l is rotated about one end perpendicular to the magnetic field B with constant angular velocity omega . The induced e.m.f between the two ends is
View SolutionA horizontal rod of length 'l' rotates about a vertical axis with a uniform angular velocity 'omega' . A uniform magnetic field of induction B exists parallel to the axis of rotation. The potential different between the ends of the rod is
View SolutionA copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
View Solution

