Two particles are thrown from the same point with the same velocity of 49ms−1. First is projected making angle θ with the horizontal and second at an angle (90∘−θ). The second particle is found to rise 22.5 m higher than the first. Find the height to which each particle will rise.
The correct Answer is:(50m,72.5m)
Similar Questions
Two particles are thrown with same initial speed from the same point with angles of projection420 and 480. Find relation between ranges and heights.
View SolutionTwo balls A and B are thrown from the same point with similar velocity of 19.6ms , at angle θ and 90∘−θ with the horizontal , respectively . Ball B reaches 10 m higher than ball A. Find the individual maximum higher reached by ball A and B .
View Solution
Knowledge Check
A particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
AAfter 2 s, the velocity of particle makes an angle of 60∘ with initial velocity vector.BAfter 1 s, the velocity of particles makes an angle of 60∘ with initial velocity vector.CThe magnitude of velocity of particle after 1 s is 10ms−1.DThe magnitude of velocity of particle after 1 s is 5ms−1.Two particles are projected from the same point with the same speed at different angles θ1 & θ2 to the horizontal. They have the same range. Their times of flight are t1 & t2 respectily
At1t2=tan2θ1Bt1sinθ1=t2cosθ2Ct1t2=tanθ1Dt1t2=tan2θ2A particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
A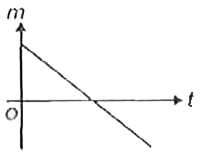 B
B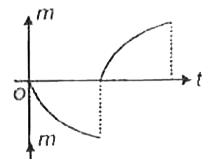 C
C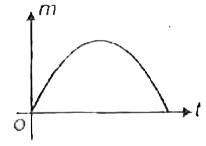 D
D
A particle of mass m is projecte dwilth speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionIf a particle is projected with a velocity 49m/s making an angle 60∘ with the horizontal, its time of flight is
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionTwo bodies are thrown with the same initial velocity at angles θ and (90∘−θ) respectively with the horizontal, then their maximum height are in the ratio
View SolutionA particle is projected with a speed u at an angle θ to the horizontal. Find the radius of curvature.
At the point where the particle is at a highest half of the maximum height H attained by it.
View Solution

