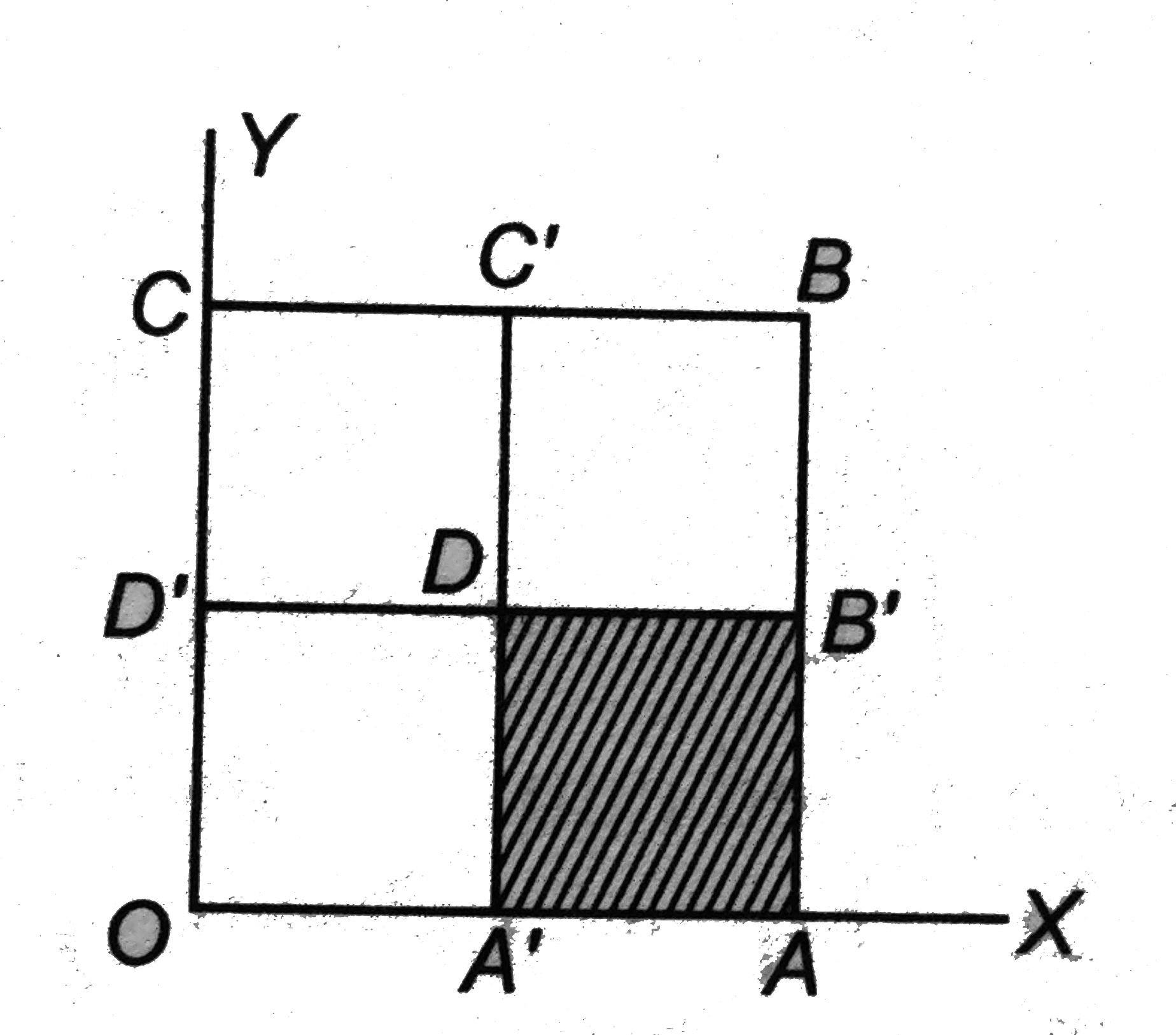
A square of side 4m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find

the position of centre of mass of the remaining portion from the centre O.
Step by step video & image solution for A square of side 4 m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find the position of centre of mass of the remaining portion from the centre O. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBook:SL ARORAChapter:ROTATIONAL MOTIONExercise:Problem
Explore 24 Videos
- ROTATIONAL MOTIONBook:SL ARORAChapter:ROTATIONAL MOTIONExercise:Problem for self practice
Explore 90 Videos
- PROPERTIES OF SOLIDSBook:SL ARORAChapter:PROPERTIES OF SOLIDSExercise:All Questions
Explore 97 Videos
- System of particles & rotational MotionBook:SL ARORAChapter:System of particles & rotational MotionExercise:EXERCISE
Explore 353 Videos
Similar Questions
An isolated particle of mass m is moving in a horizontal plane (x-y), along the x-axis at a certain height above the ground. It suddenly explodes into two fragments of masses m/4 and 3m/4. At instant later, the smaller fragment is at y=+5cm. What is the position of larger fragment at this instant ?
View SolutionThe distance between the carbon atom and the oxygen atom in a carbon monoxide molecule is 1.1Å. Given, mass of carbon atom is 12 a.m.u. and mass of oxygen atom is 16 a.m.u., calculate the position of the centre of mass of the carbon monoxide molecule
View SolutionA wire increases by 10−3 of its length when a stress of 1×108Nm−2 is applied to it. What is the Young's modulus of the material of the wire?
View SolutionTwo bodies of masses 1 kg and 2 kg are located at (1,2) and (-1,3), respectively. Calculate the coordinates of center of mass.
View SolutionA square of side 2cm and uniform thickness is divided into four squares. The square portion A′AB′D is removed and the removed portion is placed over the portion DB′BC′. The new position of centre of mass is
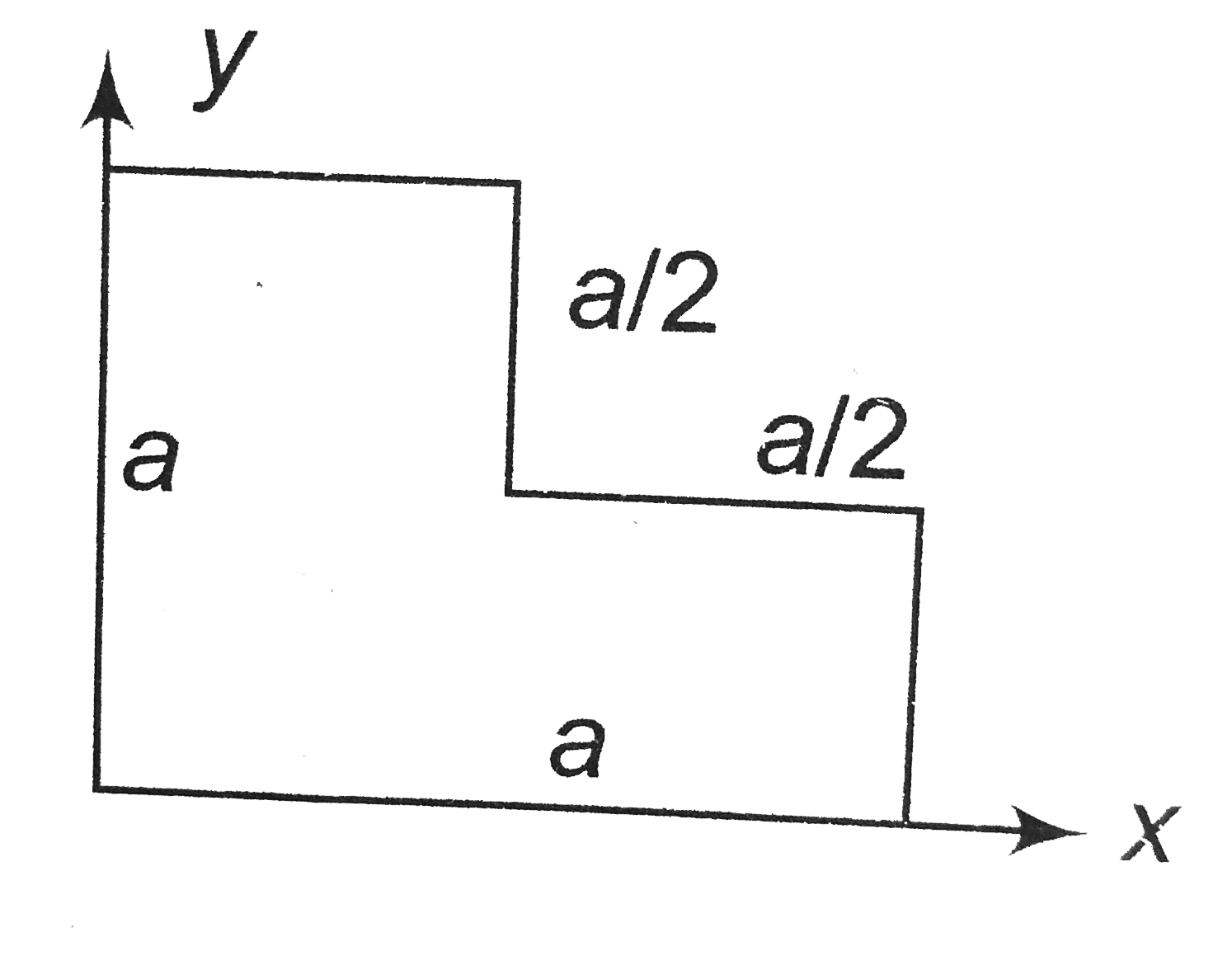
View SolutionA square of side a and uniform thickness is divided into four equal parts. If upper right part is removed, then find the coordinates of centre of mass of remaining part.
 .
.
View SolutionA square of side 4 m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find the position of centre of mass of the remaining portion from the centre O .
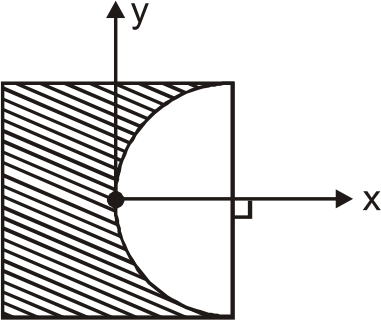
View SolutionIn the figure shown a semicircular area is removed from a uniform square plate of side l and mass ‘m’ (before removing). The x-coordinate of centre of mass of remaining portion is (The origin is at the centre of square)
View SolutionFigure shows a square plate of uniform thickness and side length sqrt 2 m . One fourth of the plate is removed as indicated. The distance of centre of mass of the remaining portion from the centre of the original square plate is
View SolutionA square plate of edge a/2 is cut out from a uniform square plate of edge 'a' shown in figure. The mass of the remaining portion is M. The moment of inertia of the shaded portion about an axis passing through 'O'( centre of the square of side a) and perpendicular to plane of the plate is :

View SolutionFour particles of masses m, m, 2m and 2m are placed at the corners of a square of side a, as shown in fig. Locate the centre of mass.
View SolutionFrom a square sheet of uniform density , a portion a removed shown shaded in fig. Find the centre of msas of the remaining portion is the side of the square is α

View SolutionFour equal masses (each of mass M) are placed at the corners of a squares side a the escape velocity of a body from the centre O of the square is
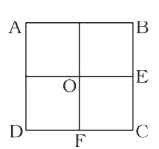
View SolutionA square of side 4 cm and of uniform thickness is divided into four equal squares. If one of them is cut off (OECF), then the position of the centre of mass of the remaining portion from O is √2kcm . Find the value of K.
View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

View SolutionA uniform square sheet has a side length of 2R. A circular sheet of maximum possible area is removed from one of the quadrants of the square sheet. The distance of centre of mass of the remaining portion from the centre of the original sheet is
View Solution
