A ring of radius R=4m is made of a highly dense material. Mass of the ring is m1=5.4×109kg distributed uniformly over its circumference. A highly dense particle of mass m2=6×108kg is placed on the axis of the ring at a distance x0=3m from the centre. Neglecting all other forces, except mutual gravitational interacting of the two. Caculate
(i) displacemental of the ring when particle is at the centre of ring, and
(ii) speed of the particle at that instant.
The correct Answer is:(a) 0.3m (b) 18m/s
Step by step video, text & image solution for A ring of radius R = 4m is made of a highly dense material. Mass of the ring is m_(1) = 5.4 xx 10^(9) kg distributed uniformly over its circumference. A highly dense particle of mass m_(2) = 6 xx 10^(8) kg is placed on the axis of the ring at a distance x_(0) = 3 m from the centre. Neglecting all other forces, except mutual gravitational interacting of the two. Caculate (i) displacemental of the ring when particle is at the centre of ring, and (ii) speed of the particle at that instant. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two objects of masses m and 4m are at rest at an infinite separation. They move towards each other under mutual gravitational attraction. If G is the universal gravitaitonal constant, then at separation r
View SolutionA ring of radius R=4m is made of a highly dense material. Mass of the ring is m1=5.4×109kg distributed uniformly over its circumference. A highly dense particle of mass m2=6×108kg is placed on the axis of the ring at a distance x0=3m from the centre. Neglecting all other forces, except mutual gravitational interacting of the two. Caculate
(i) displacemental of the ring when particle is at the centre of ring, and
(ii) speed of the particle at that instant.
View SolutionA ring has a total mass M but non-uniformly distributed over its circumference. The radius of the ring is R . A point mass m is placed at the centre of the ring. Workdone in taking away this point mass from ecntre to infinity is
View SolutionTwo identical thin ring each of radius R are co-axially placed at a distance R. If the ring have a uniform mass distribution and each has mass m1 and m2 respectively, then the work done in moving a mass m from the centre of one ring to that of the other is :
View SolutionA particle of mass m is placed at a distance R from centre of a uniformly dense thin ring of mass m rand radius R on a axis passing through its centre and perpendicular to its plane. Find the speed of the particle when it reaches at the centre fo the ring due to their mutual gravitation force.
View SolutionA ring of radius R is made from a thin wire of radius r. If ρ is the density of the material of wire then what will be the gravitational force exerted by the ring on the material particle of mass m placed on the axis of ring of ring at a distance x from its centre. Shown that the force will be maximum when x=R/√2 and the maximum value of force will be given as
Fmax=4π2Gr2ρm(3)3/2R2
View SolutionMass is non - uniformly distributed on the circumference of a ring of radius a and centre at origin . Let b be the distance of centre of mass of the ring from origin. Then ,
View SolutionMass of 20 kg is distributed uniformly over a ring of radius 2m. Find the the grvitational field at a point lies an th axis of the ring at a distance of 2 sqrt(3) m from the centre.
View SolutionMass of 10 kg is distributed uniformly over a ring of radius 1m. Find the gravitational potential at a point lies on the axis of the ring at a distance of 1m from the centre.
View SolutionA ring of radius R=8m is made of a highly dense-material Mass of the ring is mR=2.7×109kg distributed uniformly over its circumference. A particle of mass (dense) mp=3×108kg is palced on the axis of the ring speed (in cm/sec) of the particle at the instant when it passes through centre of ring .
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA conducting ring of radius 40 cm has a charge of 5 xx 10^(-9) C uniformly distributed over it. Calculate the electric field intensity at a point P, 40 cm away from the centre on the axis of the ring.
View Solutionदो एकसमान पतले वलय जिनमें प्रत्येक की त्रिज्या R है, समाक्ष पर R दूरी पर रखे हैं। यदि वलयों पर द्रव्यमान वितरण समान है तथा उनके द्रव्यमान क्रमश: m1 तथा m2 हैं, तब एक द्रव्यमान m पर एक केन्द्र से दूसरे केन्द्र तक जाने में किया गया कार्य है
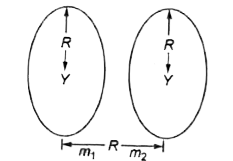
View SolutionA ring of radius R=4m is made of a highly dense material. Mass of the ring is m1=5.4×109kg distributed uniformly over its circumference. A highly dense particle of mass m2=6×108kg is placed on the axis of the ring at a distance x0=3m from the centre. Neglecting all other forces, except mutual gravitational interacting of the two. Caculate
(i) displacemental of the ring when particle is at the centre of ring, and
(ii) speed of the particle at that instant.
View SolutionMass is non - uniformly distributed on the circumference of a ring of radius a and centre at origin . Let b be the distance of centre of mass of the ring from origin. Then ,
View SolutionMass of 20 kg is distributed uniformly over a ring of radius 2m. Find the the grvitational field at a point lies an th axis of the ring at a distance of 2 sqrt(3) m from the centre.
View Solution

