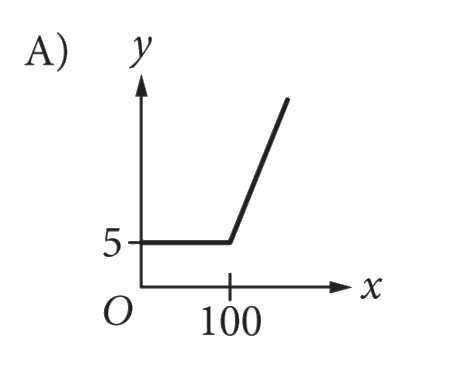
A text messaging plan charges a flat fee of $5 per month for up to 100 text messages sent plus $0.25 for each additional text message sent that month. Which of the following graphs represents the cost, y, of sending x texts in a month?
The correct Answer is:A
To solve the problem, we need to analyze the text messaging plan and determine how the cost y changes with the number of text messages sent x.
1. Understand the Pricing Structure:
- The plan charges a flat fee of $5 for up to 100 text messages.
- For any text messages sent beyond 100, there is an additional charge of $0.25 for each extra message.
2. Define the Cost Function:
- For x (the number of text messages) less than or equal to 100:
y=5
- For x greater than 100:
y=5+0.25(x−100)
- This means that for every additional text message sent beyond 100, the cost increases by $0.25.
3. Graph the Cost Function:
- For 0≤x≤100, the cost y is constant at $5. This will be a horizontal line at y=5.
- For x>100, the cost will increase linearly. The slope of this line is 0.25, starting from the point (100,5).
4. Identify the Characteristics of the Graph:
- The graph should show a horizontal line at y=5 for x from 0 to 100.
- After x=100, the graph should show a line that rises with a slope of 0.25.
5. Evaluate the Given Graph Options:
- We need to find a graph that matches the characteristics described above:
- A horizontal line at y=5 for x from 0 to 100.
- A line that increases after x=100.
6. Select the Correct Graph:
- After evaluating the options, we find that:
- Option A shows a horizontal line at y=5 for x≤100 and then a line that increases after x=100.
- Option B shows a decrease in cost after x=100, which is not possible according to the pricing structure.
Conclusion:
The correct graph that represents the cost y of sending x texts in a month is Option A.
- The plan charges a flat fee of $5 for up to 100 text messages.
- For any text messages sent beyond 100, there is an additional charge of $0.25 for each extra message.
- For x (the number of text messages) less than or equal to 100:
y=5
- For x greater than 100:
y=5+0.25(x−100)
- This means that for every additional text message sent beyond 100, the cost increases by $0.25.
- For 0≤x≤100, the cost y is constant at $5. This will be a horizontal line at y=5.
- For x>100, the cost will increase linearly. The slope of this line is 0.25, starting from the point (100,5).
- The graph should show a horizontal line at y=5 for x from 0 to 100.
- After x=100, the graph should show a line that rises with a slope of 0.25.
- We need to find a graph that matches the characteristics described above:
- A horizontal line at y=5 for x from 0 to 100.
- A line that increases after x=100.
- After evaluating the options, we find that:
- Option A shows a horizontal line at y=5 for x≤100 and then a line that increases after x=100.
- Option B shows a decrease in cost after x=100, which is not possible according to the pricing structure.
The correct graph that represents the cost y of sending x texts in a month is Option A.
Similar Questions
Max's cell phone plan charges a monthly "pay-as-you-go rate" of $0.13 for each text message sent or received. If Max was charged $7.41 for 15 more sent texts than he received, how many texts did Max send?
View SolutionOn January 1, a share of a certain stock costs of $180. Each month decreased by one-third. If x represents the time, in months, and y represents the cost of the stock, in dollars, which graph best represents the cost of a share over the following 5 months?
View Solution
Knowledge Check
Gina subscribes to a cell phone service that charges a monthly fee of $60.00. The first 500 megabytes of data is free, and the cost is $0.15 for each additional megabyte of data used that month. Which of the following functions gives the cost, in dollars, for a month in which Gina uses x megabytes of data, where x>500.
A60+15xB0.15x−15C0.15x−440D60+0.15xA yoga studio charges a one-time registration fee of $75 plus montly membership fee of $45. if the montly fee is subject to a sales tax of 6%, which of the following expressions represents the total cost of membership for n months?
A(45×1.06×75)nB45(1.06)n+75C(75+45)(0.06)+45nD(45+0.06)n+75On Saturday afternoon, Armand sent m text messages each hour for 5 hours, and Tyrone sent p text messages each hour for 4 hours. Which of the following represents the total number of messages sent by Armand and Tyrone on Saturday afternoon?
A9mpB20mpC5m+4pD4m+5p
One of the requirements for becoming a court reporter is the ability to type 225 words per minute. Donald can currently type 180 words per minute, and believes that with practice he can increase his typing speed by 5 words per minute each month. Which of the following represents the number of words per minute that Donald believes he will be able to type m months from now?
View SolutionC=60+0.25d
The equation represents the monthly cost of a cell phone that includes up to 1 gigabyte of data after which there is a charge for d gigabytes of any additional data. Which of the following must be true?
I. The cost of each additional megabyte of data is $60.25.
II. The y-intercept of the graph of the cost equation represents the charge for each additional megabytes of data used.
III. If betwee 5 and 6 megabytes of data are used in month, the monthly charge is $61.25.
View SolutionJoseph joins a gym that charges $79.99 per month plus tax for a premium membership. A tax of 6% is applied to the monthly fee. Joseph is also charged a one-time initiation fee of $95 as soon as he joins. There is no contract so that Joseph can cancel at any time without having to pay a penalty. Which of the following represents Joseph’s total charge, in dollars, if he keeps his membership for t months?
View SolutionThe friends start an international club that meets monthly . To increase membership, they decide that at the next meeting . Each member will being a friend , and at each subsequent meeting for the next 6 months. Each member will bring a new member . For this plan , whic of the following graphs , for x gt 0 , represents the number of members after x meetings ?
View SolutionMelanie puts $1,100 in an investment account that she expects will make 5% interests for each three month period. However, after a year she realizes she was wrong about the interest rate and she has $50 less than she expected. Assuming the interest rate the account earns is constant, which of the following equations expresses the total money ,x, she will after t years using the actual rate?
View Solution

