A spherical body of radius R rolls on a horizontal surface with linear velociltly v. Let L1 and L2 be the magnitudes of angular momenta of the body about centre of mass and point of contact P. Then:
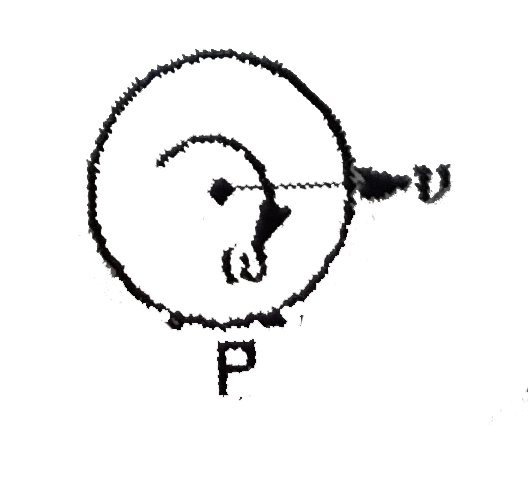
L2=2L1, if radius of gyration about centroidal axis K=R
L2=2L1, for all cases
L2<2L1, if radius of gyration about centroidal axis K<R
L2<2L1, if radius of gyration about centroidal axis K>R
The correct Answer is:A, C
Step by step video, text & image solution for A spherical body of radius R rolls on a horizontal surface with linear velociltly v. Let L_(1) and L_(2) be the magnitudes of angular momenta of the body about centre of mass and point of contact P. Then: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A solid sphere is rolling on a horizontal surface such that speed of the centre of sphere is u. Mase of the sphere is m and radius R. Magnitude of angular momentum about the point of contact is found to be (7)/(n)mvR /. Find the value of n
View SolutionTwo rotating bodies A and B of masses m and 2 m with moments of inertia IA and IB(IB>IA) have equal kinetic energy of rotation . If LA and LB be their angular momenta respectively , then
View SolutionA symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v_0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA body of radius R and mass m is rolling smoothly with speed v on a horizontal surface. It then rolls up a hill to a maximum height h. If h=3v2/4g. What might the body be ?
View SolutionIn the figure shown mass of both, the spherical body and blocks is m. Moment of inertia of the spherical body about centre of mass is 2mR^(2) . The spherical body rolls on the horizontal surface. There is no sliping between any two surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is
View SolutionA spherical body of radius R rolls on a horizontal surface with linear velociltly v. Let L1 and L2 be the magnitudes of angular momenta of the body about centre of mass and point of contact P. Then:
View SolutionIn the figure shown mass of both, the spherical body and block is m. Moment of inertia of the spherical body about centre of mass is 2mR2. The spherical body rolls on the horizontal surface. There is no slipping at any surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is
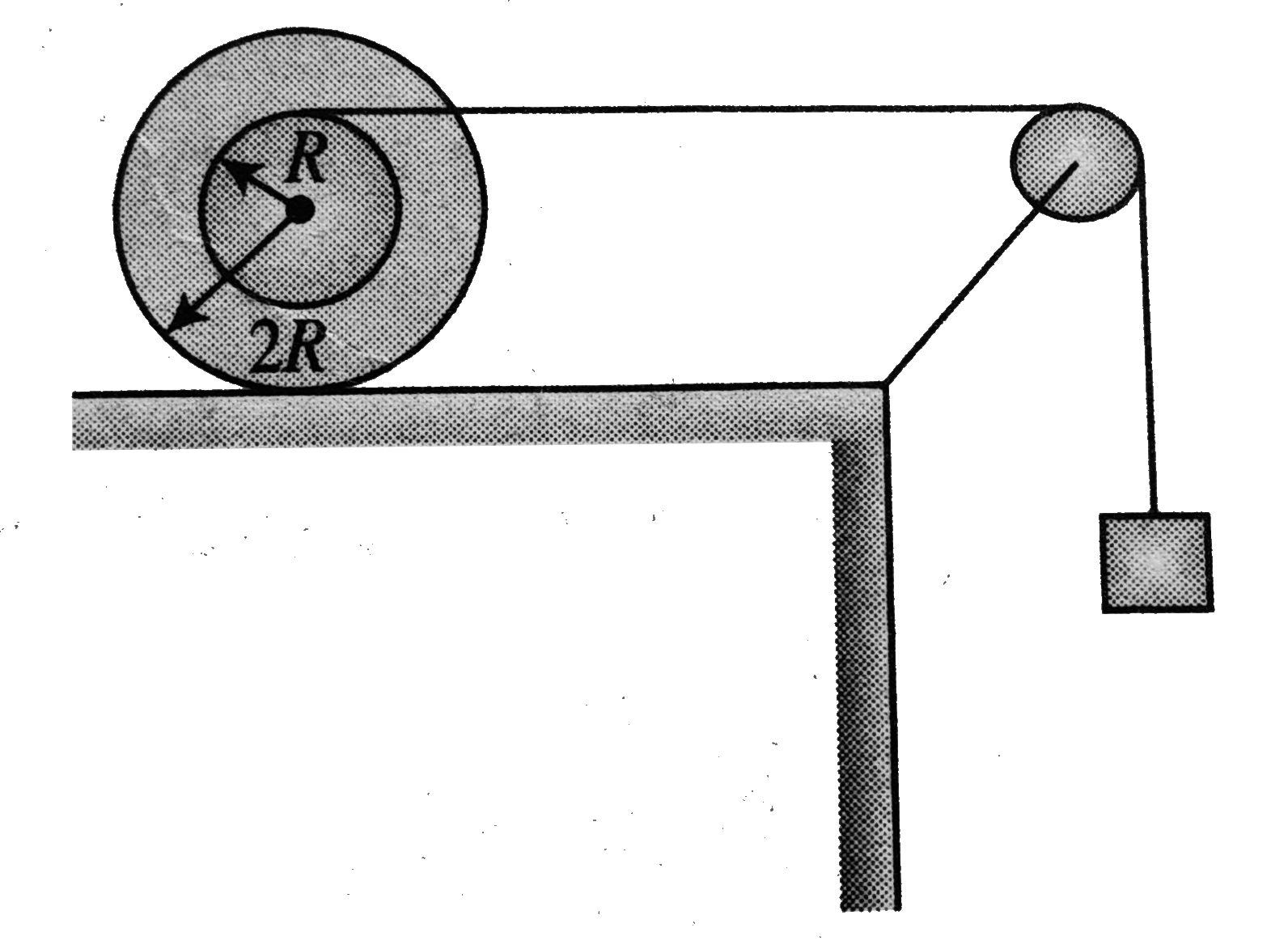
View Solution

