Heat is conducted through a slab composed of paralel layers of two different materials of conductivities 134.4 SI units and 58.8 SI units and of thickness 3.6cm and 4.2cm respectively. The temperature of the outer faces of the compound slab are 96∘C and 8∘C. Find (i) the temperature of the interface, (ii) temperature gradient in each section of the slab.
The correct Answer is:1523.8∘C per metre
To solve the problem, we will use the concept of thermal conduction through materials and the formula for temperature gradient. The temperature gradient (dT/dx) is defined as the change in temperature (ΔT) over the change in distance (Δx).
Given Data:
- Conductivity of material 1 (k1) = 134.4 SI units
- Conductivity of material 2 (k2) = 58.8 SI units
- Thickness of material 1 (L1) = 3.6 cm = 0.036 m
- Thickness of material 2 (L2) = 4.2 cm = 0.042 m
- Temperature at the outer face of the slab (T1) = 96°C
- Temperature at the outer face of the slab (T2) = 8°C
Step 1: Calculate the temperature at the interface (T)
For steady-state conduction through parallel layers, the heat flow (Q) through each layer is equal. We can express this as:
T1−TL1⋅k1=T−T2L2⋅k2
Substituting the known values:
96−T0.036⋅134.4=T−80.042⋅58.8
Step 2: Rearranging the equation
Multiply both sides by 0.036⋅0.042 to eliminate the denominators:
(96−T)⋅134.4⋅0.042=(T−8)⋅58.8⋅0.036
Step 3: Simplifying the equation
Now, we will simplify both sides:
Left side:
134.4⋅0.042=5.6448
So,
(96−T)⋅5.6448=(T−8)⋅2.1168
Right side:
58.8⋅0.036=2.1168
Step 4: Expanding the equation
Expanding both sides gives us:
96⋅5.6448−T⋅5.6448=T⋅2.1168−8⋅2.1168
Step 5: Collecting like terms
Now, we will collect all terms involving T on one side:
96⋅5.6448+8⋅2.1168=T⋅(5.6448+2.1168)
Step 6: Solving for T
Now we can calculate T:
1. Calculate 96⋅5.6448 and 8⋅2.1168.
2. Add these results together.
3. Divide by 5.6448+2.1168 to find T.
Step 7: Calculate the temperature gradients
Now that we have T, we can calculate the temperature gradients in each section.
For Material 1:
Temperature Gradient (G1)=T1−TL1=96−T0.036
For Material 2:
Temperature Gradient (G2)=T−T2L2=T−80.042
Final Calculation
1. Substitute the value of T into the equations for G1 and G2.
2. Calculate the gradients.
Summary of Results:
- (i) The temperature at the interface (T).
- (ii) The temperature gradients in each section (G1 and G2).
- Conductivity of material 1 (k1) = 134.4 SI units
- Conductivity of material 2 (k2) = 58.8 SI units
- Thickness of material 1 (L1) = 3.6 cm = 0.036 m
- Thickness of material 2 (L2) = 4.2 cm = 0.042 m
- Temperature at the outer face of the slab (T1) = 96°C
- Temperature at the outer face of the slab (T2) = 8°C
For steady-state conduction through parallel layers, the heat flow (Q) through each layer is equal. We can express this as:
Multiply both sides by 0.036⋅0.042 to eliminate the denominators:
Now, we will simplify both sides:
134.4⋅0.042=5.6448
So,
(96−T)⋅5.6448=(T−8)⋅2.1168
58.8⋅0.036=2.1168
Expanding both sides gives us:
Now, we will collect all terms involving T on one side:
Now we can calculate T:
2. Add these results together.
3. Divide by 5.6448+2.1168 to find T.
Now that we have T, we can calculate the temperature gradients in each section.
Temperature Gradient (G1)=T1−TL1=96−T0.036
Temperature Gradient (G2)=T−T2L2=T−80.042
1. Substitute the value of T into the equations for G1 and G2.
2. Calculate the gradients.
- (i) The temperature at the interface (T).
- (ii) The temperature gradients in each section (G1 and G2).
Similar Questions
A wall consists of two layer, one of thickness 3 cm and other of 6 cm. the thermal conductivities of the materials of these layers are K and 3K respectively. The temperature of the outer surfaces of the two layers are −5∘C and 20∘C respectively. determine the temperature of the surface of contact of the two layers in the steady state.
View SolutionA slab consists of two parallel layers of different materials 4cm and 2cm thick and of thermal conductivities 54cals−1m−1K−1 and 36cals−1m−1K−1 respectively. If the faces of the slab are at 100∘C and 0∘C calculate the temperature of the surface dividing the two materials.
View Solution
Knowledge Check
Two bars of thermal conductivities K and 3K and lengths 1cm and 2cm respectively have equal cross-sectional area, they are joined lengths wise as shown in the figure. If the temperature at the ends of this composite bar is 0∘C and K2/l respectively (see figure), then the temperature ϕ of the interface is
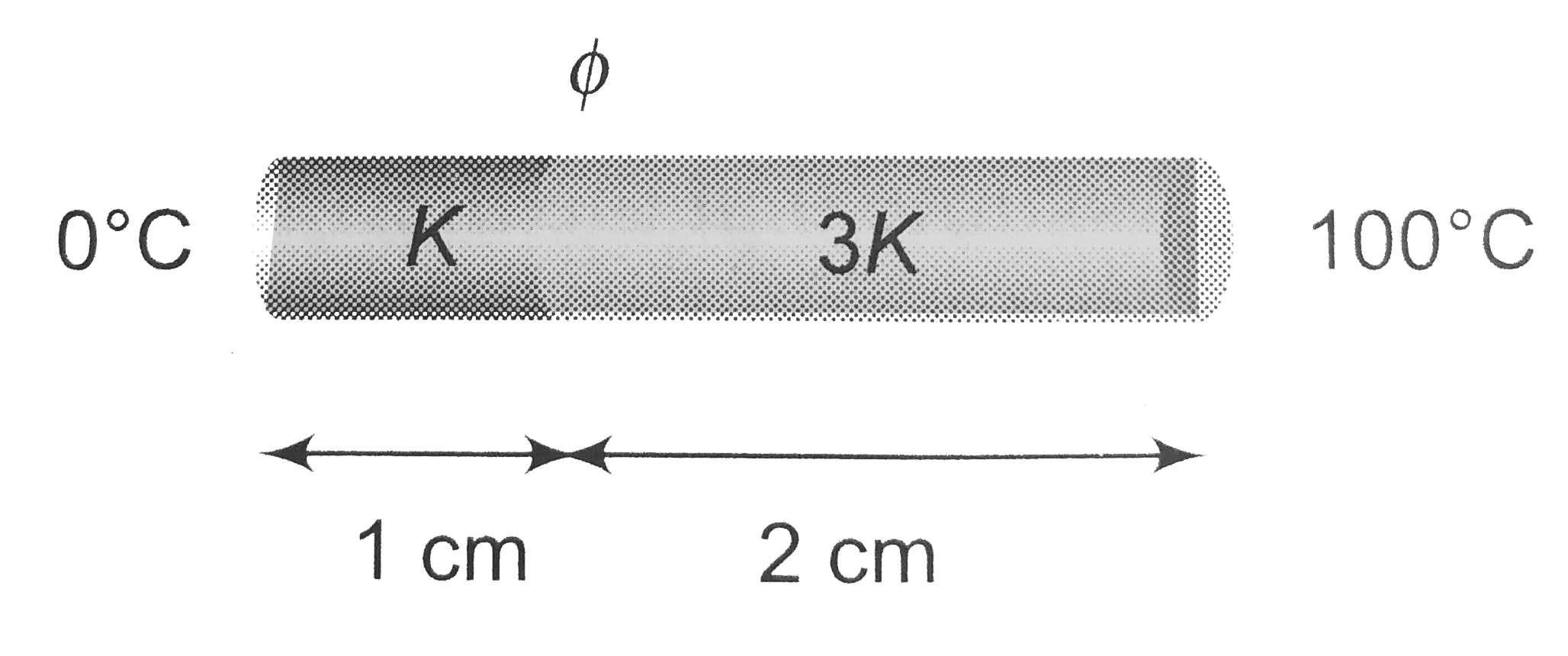 A50∘CB1003.∘CC60∘CD2003.∘C
A50∘CB1003.∘CC60∘CD2003.∘CA compound slab is made of two parallel plates of copper and brass of the same thickness and having thermal conductivities in the ratio 4:1. The free face of copper is at 0∘C. The temperature of the internal is 20∘C. What is the temperature of the free face of brass?
A0∘CB20∘CC40∘CD100∘C
A composite wall of area A is made of equal thickness of lead and iron having thermal conductivities K and 2K, respectively. The temperature on the two sides of the composite wall are 100∘C and 0∘C with the layer on the hotter side. Calculate the steady -state temperature of the lead-iron interface.
View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
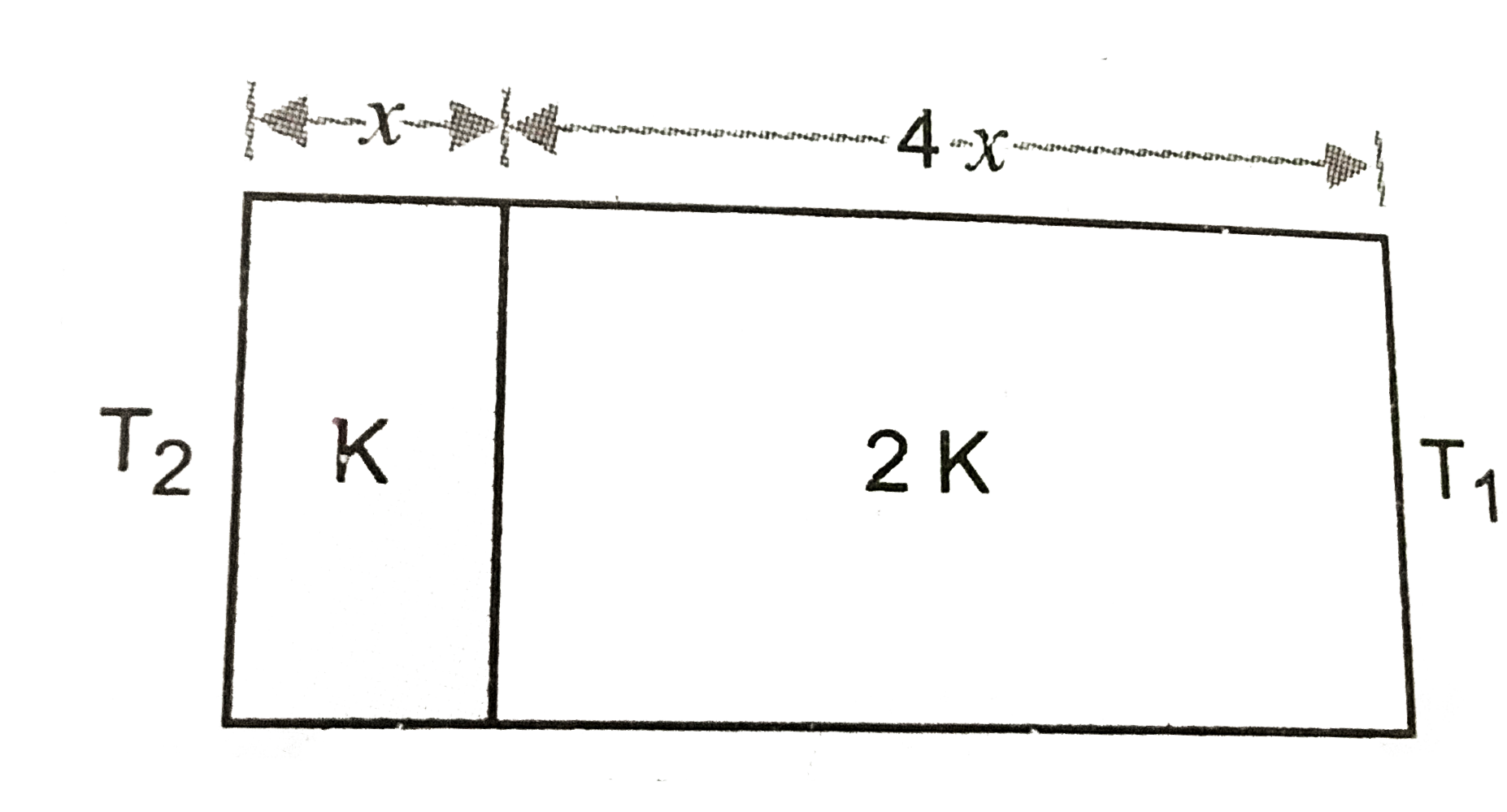
View SolutionTwo materials having coefficients of thermal conductivity ‘3 K’ and ‘K’ and thickness ‘d’ and ‘3 d’, respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are θ2 and θ1 respectively, (θ2>θ1) The temperature at the interface is:
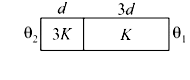
View SolutionHeat is supplied to a slab of cork, 5cm thick and of 2m2 by a heating coil spread over its surface. When the current in the coil is 1.18 A and the potential difference across its end is 20 V, the steady temperatures of the faces of the slab are 12.5∘C and 0∘C. Assuming that the whole of the heat developed in the coil is conducted through the slab, calculate the thermal conductivity of the cork.
View SolutionHeat is flowing through a rod of length 25.0cm having cross-sectional area 8.80cm2. The coefficient of thermal conductivity for the material of the rod is K=9.2×10−2kcals−1m−1.∘C−1. The Temperatures of the ends of the rod are 125∘C and 0∘C in the steady state. Calculate (i) temeprature gradient in the rod (ii) temperature of a point at a distance of 10.0cm from the hot end and (iii) rate of flow of heat.
View SolutionTwo walls of thickness in the ratio 1:3 and thermal conductivities in the ratio 3:2 form a composite wall of a building. If the free surfaces of the wall be at temperatures 30∘C and 20∘C, respectively, what is the temperature of the interface?
View Solution
