Let x and y be numbers such that - y<x<y. Which of the following must be true?
I.|x|<y
II.X>0
III.Y>0
I only
I and II only
I and III only
I, II, and III
The correct Answer is:C
To solve the problem, we have the inequality given as:
−y<x<y
We need to analyze the three statements to determine which must be true based on this inequality.
Step 1: Analyze the inequality
From the inequality −y<x<y, we can derive some information about x and y.
1. The left part of the inequality −y<x implies that x is greater than −y.
2. The right part of the inequality x<y implies that x is less than y.
Step 2: Check the first statement: |x|<y
To check if |x|<y must be true, we can analyze the bounds on x:
- Since x<y, we know that x cannot be equal to or greater than y.
- If x is negative (which it can be, since x can be less than y), then |x|=−x.
Now, since −y<x<y, let's consider the case where x is negative.
- If x is negative, then |x|=−x and since −y<x, we can say that −x<y. Thus, |x|<y holds true.
If x is positive, then |x|=x and since x<y, it also holds that |x|<y.
Thus, the first statement is true.
Step 3: Check the second statement: x>0
The inequality −y<x<y does not guarantee that x is positive.
- For example, if we take y=3 and x=−2, then −3<−2<3 holds true, but x is not greater than 0.
Thus, the second statement is not necessarily true.
Step 4: Check the third statement: y>0
The inequality −y<x<y implies that y must be positive.
- If y were negative or zero, then −y would be positive or zero, which would contradict the inequality −y<x because x would have to be less than or equal to zero in that case.
Thus, y must be greater than 0.
Conclusion
Based on the analysis, we conclude that:
- Statement I: |x|<y is true.
- Statement II: x>0 is not necessarily true.
- Statement III: y>0 is true.
Therefore, the statements that must be true are I and III.
Final Answer
The statements that must be true are:
- I. |x|<y
- III. y>0
2. The right part of the inequality x<y implies that x is less than y.
- If x is negative (which it can be, since x can be less than y), then |x|=−x.
- Statement II: x>0 is not necessarily true.
- Statement III: y>0 is true.
- I. |x|<y
- III. y>0
Similar Questions
Knowledge Check
Let a and b be numbers such that −a<b+1<a. Which of the following must be true ?
I. a>0
II. |b|<a
III. b>a+1AI onlyBI and IICII onlyDI, II, and IIIIf x+y=90∘, which of the following must be true?
Acosx=cosyBsin x=-sin yCtan x=cot yDsin x+cos y=1If ab>0, then which one of the following must be true?
Aa/b>0Ba−b>0Ca+b>0Db−a>0
If x+z>y+z, then which of the following must be true?
View Solution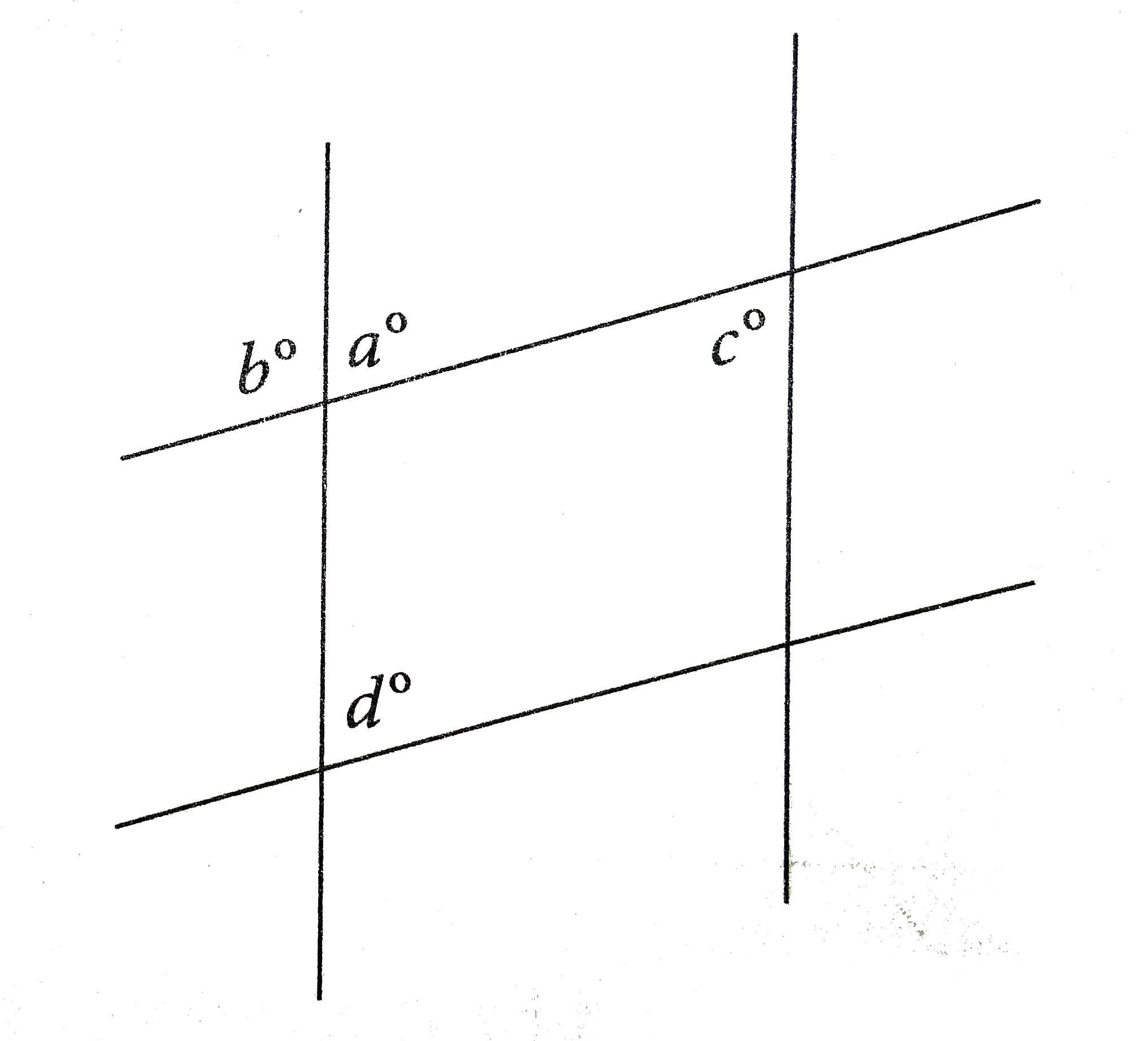
Which of the following statements must be true?
I. a+b<180
II. a+d=180
III.a+d>180
View SolutionIF x+y=0, which of the following must be equivalent to x-y?
View SolutionIf x5+x2<0, then which one of the following must be true?
View SolutionIf a=3+b, which of the following must be true?
I. a>b+2.5
II. a<b+2.5
III. a>2+b
View Solution
