Derive an expression for torque on a current loop placed in a magnetic field . Solution in Tamil
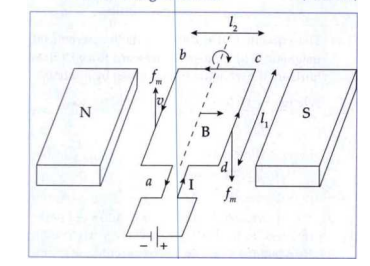
Consider a single rectangular loop PQRS kept in a uniform magnetic field →B . Let a and b be the length and breadth of the rectangular loop respectively . Let ˆn be the unit vector normal to the plane of the current loop . This unit vector ˆn completely describes the orientation of the loop.
Let →B directed from north pole to south pole of the magnet as shown in Figure.

When an electric current is sent through the loop , the net force acting is zero but there will be net torque acting on it. For the sake of understanding, we shall consider two configurations of the loop ,
(i) unit vector ˆn points perpendicular to the field (ii) unit vector points at an angle θ with the field.
when unit vector ˆn is perpendicular to the field
In the simple configuration , the unit vector ˆn is perpendicular to the field and plane of the loop is lying on xy plane as shown in Figure. Let the loop be divided into four sections PQ, QR , RS and SP. The Lorentz force on each loop can be calculated as follows :
(a) Force on section PQ ,
→i=−aˆj and →B=Bˆi
→FPQ=→Il×→B(ˆj׈i)=IaBˆk
Since the unit vector normal to the plane ˆn is along the direction of ˆk
(b) The force on section QR
→l=→bi and →B=Bˆi
→FQR=→Il×→B=−IbB(ˆi׈i)=→0
( c ) The force on section RS
→l=aˆj and →B=Bˆi
→FRS=→Il×→B=IaB(ˆj׈i)=−IaBˆk
Since, the unit vector normal to the plane is along the direction of −ˆk .
(d) The force on section SP
→l=−bˆj and →B=Bˆi
→FSP=→Il×→B=−IbB(ˆi׈i)=→0
The net force on the rectangular loop is
→Fnet=→FPQ+→FFS+→FSP
→Fnet=IaBˆk+→0−IaBˆk+→Fnet=→0
Hence, the net force on the rectangular loop in this configuration is zero . Now let us calculate the net torque due to these dorces about an axis passing through the center
→τnet=4∑i=1→τi=4∑i=1→ri×→Fi
=(b2IaB+0+b2IaB+0)ˆj
→τnet=abIBˆj
Since, A = ab is the area of the rectangular loop PQRS, therefore, the net torque for this configuration is
→τnet=ABIˆj
Similar Questions
Derive an expression for the torque acting on a rectangular current carrying loop suspended in a uniform magnetic field.
View SolutionDerive an expression for torque acting on a barmagnet placed in magnetic field
View SolutionDerive an expression for torque acting on a bar magnet placed in a uniform magnetic field.
View SolutionDerive an expression for Torque acting on a bar magnet placed in a uniform magnetic field.
View SolutionDerive the expression for magnetic field at a point on the axis of a circular current loop.
View SolutionDerive an expression for torque acting on a rectangular current loop carrying coil placed in a uniform magnetic field.
View SolutionA rectangular loop of area A and carrying a steady current I is placed in a uniform magnetic field:-Derive the expression of torque, tau = barmxxbarB acting on the loop.
View SolutionA rectangular loop carrying a steady current is placed in a uniform magnetic field. Obtain the expression for the torque acting on the loop.
View Solution
