A needle 10 cm long is placed along the axis of a convex lens of focal length 10 cm such that the middle point of the neddle is at a distance of 10 cm from the lens. Find the length of the image of the neddle.
The correct Answer is:13.33 cm
To find the length of the image of a needle placed along the axis of a convex lens, we will follow these steps:
Step 1: Understand the setup
- We have a needle that is 10 cm long.
- The middle point of the needle is placed 10 cm away from the lens.
- The focal length of the convex lens is also 10 cm.
Step 2: Determine the positions of the ends of the needle
- Since the needle is 10 cm long, if the middle point is at 10 cm from the lens, the ends of the needle will be:
- Point A (one end) is at 10cm−5cm=5cm from the lens.
- Point B (the other end) is at 10cm+5cm=15cm from the lens.
Step 3: Use the lens formula to find the image positions
The lens formula is given by:
1V−1U=1F
Where:
- V is the image distance,
- U is the object distance (negative for real objects),
- F is the focal length.
For Point A:
- The object distance UA=−5cm (since it's on the same side as the object).
- The focal length F=10cm.
Using the lens formula:
1VA=1UA+1F
1VA=1−5+110
1VA=−210+110=−110
VA=−10cm
For Point B:
- The object distance UB=−15cm.
Using the lens formula:
1VB=1UB+1F
1VB=1−15+110
1VB=−230+330=130
VB=30cm
Step 4: Calculate the length of the image
The length of the image of the needle is given by the distance between the images of points A and B:
Length of image=|VB−VA|=|30−(−10)|=|30+10|=40cm
Conclusion
The length of the image of the needle is 40cm.
---
- We have a needle that is 10 cm long.
- The middle point of the needle is placed 10 cm away from the lens.
- The focal length of the convex lens is also 10 cm.
- Since the needle is 10 cm long, if the middle point is at 10 cm from the lens, the ends of the needle will be:
- Point A (one end) is at 10cm−5cm=5cm from the lens.
- Point B (the other end) is at 10cm+5cm=15cm from the lens.
The lens formula is given by:
1V−1U=1F
Where:
- V is the image distance,
- U is the object distance (negative for real objects),
- F is the focal length.
- The object distance UA=−5cm (since it's on the same side as the object).
- The focal length F=10cm.
1VA=1UA+1F
1VA=1−5+110
1VA=−210+110=−110
VA=−10cm
- The object distance UB=−15cm.
1VB=1UB+1F
1VB=1−15+110
1VB=−230+330=130
VB=30cm
The length of the image of the needle is given by the distance between the images of points A and B:
Length of image=|VB−VA|=|30−(−10)|=|30+10|=40cm
The length of the image of the needle is 40cm.
Similar Questions
A convex lens has a focal length of 10 cm. The object of height 2 mm is placed at a distance of 5 cm from the pole. Find the height of the image.
View Solution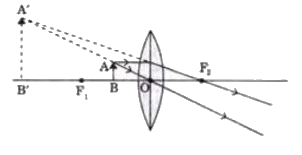
The above lens has a focal length of 10 cm. The object of height 2 mm is placed at a distance of 5 cm from the pole. Find the height of the image.
View Solution
Knowledge Check
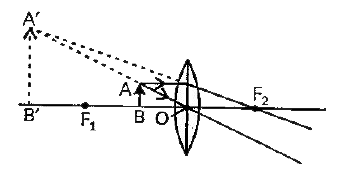
The above lens has a focal length of 10 cm. The object of height 2 mm is placed at a distance of 5 cm from the pole. Find the height of the image.A4 cmB6.67 mmC4 mmD3.33 mmA convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
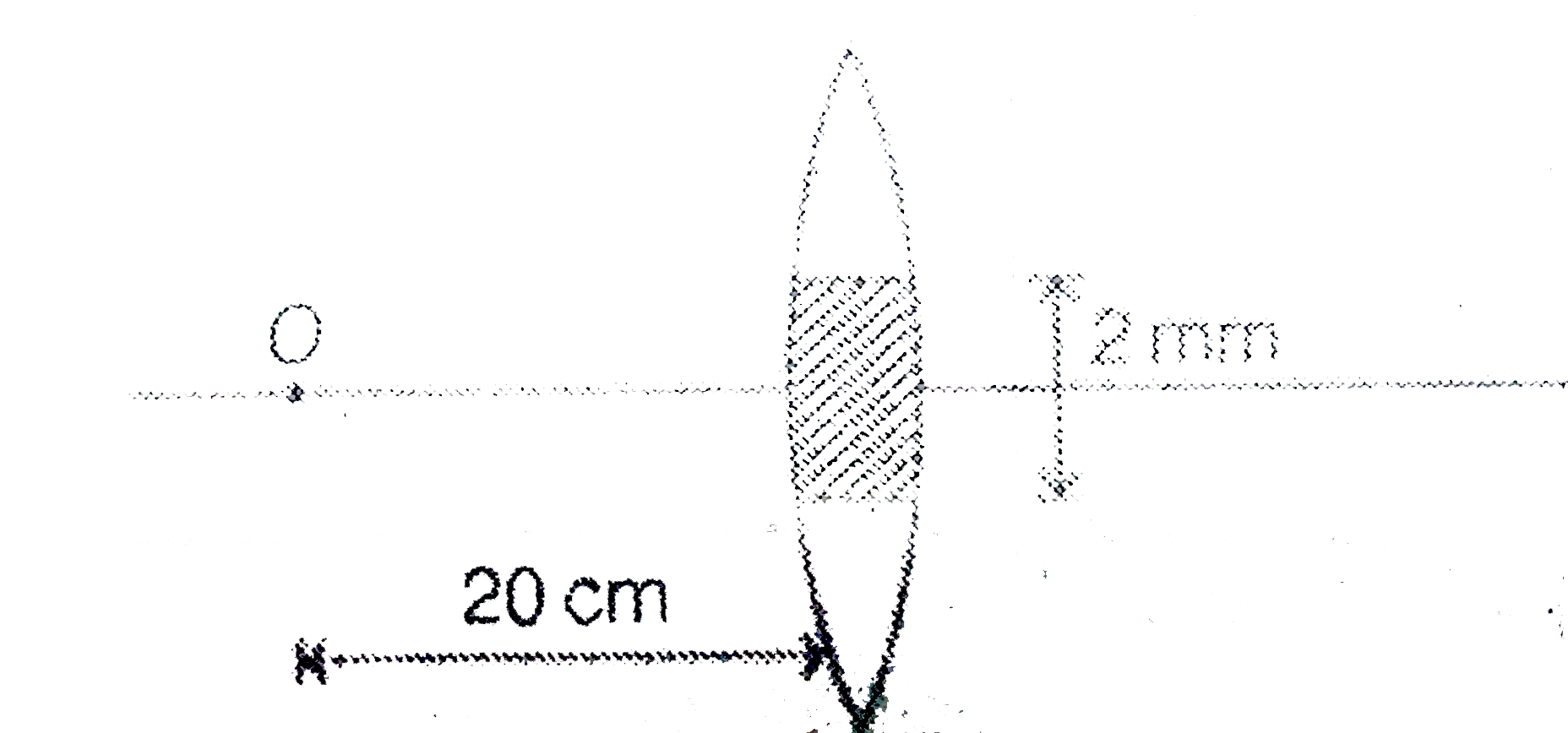 Aonly one image will be formed by the lensBthe distance between the two images formed by such a lens is 6 mmCthe distance between the images is 4 mmDthe distance between the images is 2mm
Aonly one image will be formed by the lensBthe distance between the two images formed by such a lens is 6 mmCthe distance between the images is 4 mmDthe distance between the images is 2mmA point object is placed at a distance of 12cm from a convex lens of focal length 10cm. On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
A20cmB25cmC15cmD30cm
An object 50cm tall is placed on the principal axis of a convex lens. Its 20cm tall image is formed on the screen placed at a distance of 10cm from the lens. Calculate the focal length of the lens.
View SolutionAn object 50 cm tall is placed on the principle axis of a convex lens. Its 20 cm tall image is formed on the screen placed at a distance of 10 cm from the lens. Calculate the focal length of the lens.
View SolutionThere is a convex lens of focal length 20 cm. An object of height 3 cm is placed perpendicular to principal axis of lens at a distance 10 cm from the lens. Find the size of image.
View SolutionAn object is kept at a distance of 15 cm from a convex lens of focal length 10 cm. Calculate the image distance and state the characteristics of the image formed.
View SolutionAn object is placed at a distance of 20 cm from a convex lens of focal length 10 cm . The image is formed on the other side of the lens at a distance
View Solution
