If a particle starts moving along x-axis from origin with initial velocity u=2m/s and acceleration 4m/s2 the relation between displacement and time is given as x=2t+2t2. Draw the displacement time graph for t ul(gt)0.
x=2(t2+t)=2(t2+t+14−14)
=2(t+12)2−14
∴(x+14)=2(t+12)2
∴ Vertex is(−12,−12)
and axis is t=−12
∴ Graph is

As graph is to be plotted for t>––––0
So, graph will be.

Similar Questions
If a particle starts moving along x-axis from the origin with initial velocity u=1ms−1 and acceleration a=2ms−2, the relationship between displacement and time is
x=ut+12at2=1×t+12×2×t2=t+r2
Draw the displacement (x)-time (t) graph.
View SolutionIf a particle starts moving with initial velocity u=1ms−1 and acceleration a=2ms−2, the veloctiy of the particle at any time is given by v=u+at=1+2t. Plot the velocity-time graph of the particle.
View Solution
Knowledge Check
Relation between displacement x and time t is x=2−5t+6t2, the initial acceleration will be :-
A−3ms−2B12ms−2C2ms−2D−5ms−2If a particle starts moving along a straight ine withinitial velocity u under contact acceleration a, its displacement with time is given by the relation x=ut+12at2
Q. The concerned deviation of positon time realtion w.r.t will be. Differentiation of above result w.r.t. t will beAaBu+aCuDnoneThe displacement of a particle in time t is given by s=2t2−3t+1. The acceleration is
A1B3C4D5
A particle is moving with initial velocity 1m/s and acceleration a=(4t+3)ms2. Find velocity of particle at t=2sec.
View SolutionA particle is moving along the x-axis. Consider it’s a-t graph. If initial velocity is 10 m//s, sketch the v-t graph and calculate the displacement in the time interval t=0 to 12 s.
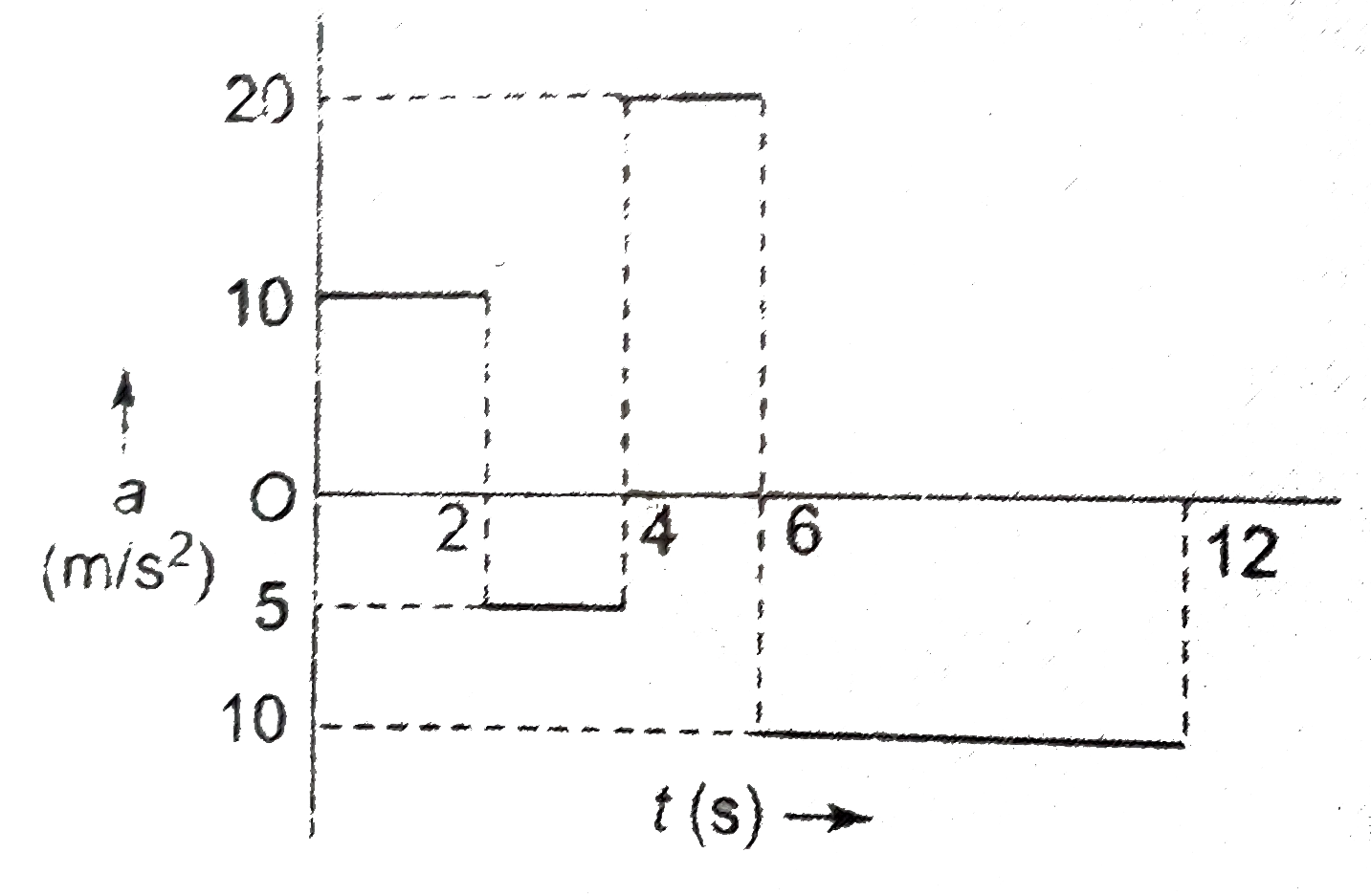
View SolutionThe displacement of a particle along the x-axis is given by x=3+8t+7t2. Obtain its velocity and acceleration at t=2s.
View SolutionWrite the relation between time period T, displacement x and acceleration a of a particle in S.H.M.
View SolutionThe acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
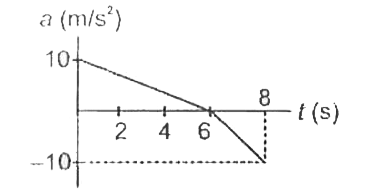
View Solution
