Two blocks A and B of masses 3 kg and 6 kg are connected by a massless spring of force constant 1800 N m−1 and then they are placed on a smooth horizontal surface. The blocks are pulled apart to stretch the spring by 5 cm and then released. What is the relative velocity (in ms−1) of the blocks when the spring comes to its natural length?
The correct Answer is:1.5
Step by step video, text & image solution for Two blocks A and B of masses 3 kg and 6 kg are connected by a massless spring of force constant "1800 N m"^(-1) and then they are placed on a smooth horizontal surface. The blocks are pulled apart to stretch the spring by 5 cm and then released. What is the relative velocity (in ms^(-1)) of the blocks when the spring comes to its natural length? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Two blocks A and B of masses m and 2m, respectively , are connected by a massless spring of force constant k and are placed on a smooth horizontal plane. The spring is stretched by an amount x and then released . The relative velocity of the blocks when the spring comes to its natural length is

View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View Solution
Knowledge Check
Two blocks of masses 6 kg and 3 kg are attached to the two ends of a massless spring of spring constant 2π2N/m. If spring is compressed and released on a smooth horizontal surface then find the time period (in seconds) of each block.
A1B2C3D4Two blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
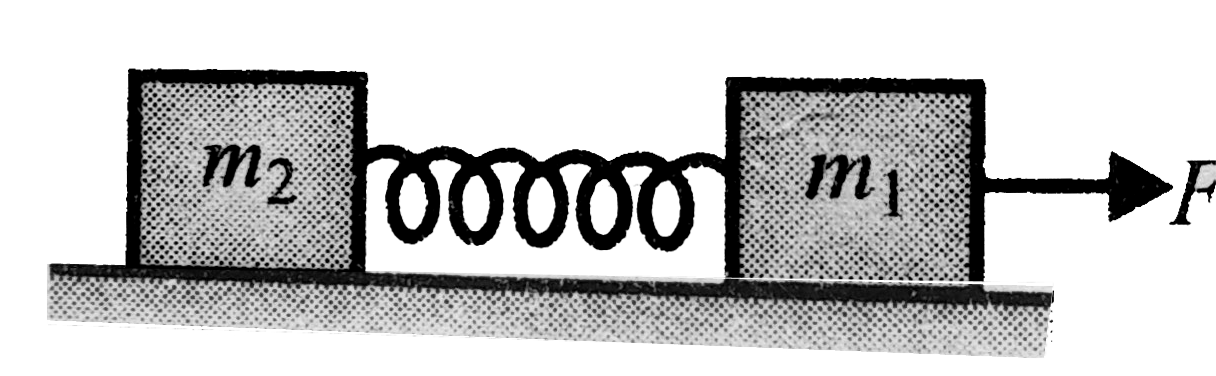
What is maximum elongation of spring.A2m1F(m1+m2)kBm21F2(m1+m2)kC2m2Fk(m1+m2)Dm22F2(m1+m2)2kTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of osciallation is
A2 cmB1 cmC3 cmD4 cm
Two blocks A and B of masses 1kg and 2kg are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Find the ratio of their,
(a) speed
(b) magnitude of momentum and
(c) kinetic energy at any instant.
View SolutionTwo blocks A and B of masses mA and mB are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Show that the kinetic energies of the blocks are, at any instant inversely proportional to their masses.
View SolutionTwo blocks of masses 10 kg and 20 kg are connected by a massless spring and are placed on a smooth horizontal surface. A force of 200 N is applied on 20 kg mass as shown in the diagram. At the instant, the acceleration of 10 kg mass is 12ms−2, the acceleration of 20 kg mass is:

View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a massless spring of spring constant K. This system lies over a smooth horizontal surface. At t=0 the bolck A has velocity u towards right as shown while the speed of block B is zero, and the length of spring is equal to its natural length at that at that instant.

Column IColumn II(A)The velocity of block A(P)can never be zero(B)The velocity of block B(Q)may be zero at certain instants of time(C)The kinetic energy of system of two block(R)is minimum at maximum compression of spring(D)The potential energy of spring(S)is maximum at maximum extension of spring
View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View Solution
