The imaginary number "I" is such that i2=−1. Which of the following statements is true about the complex number equivalent to (4−i)×(1+2i)+(1−i)×(2−3i)?
It lies on the real axis
It lies in the first quadrant
It lies in the second quadrant
It lies in the third quadrant
The correct Answer is:B
To solve the expression (4−i)(1+2i)+(1−i)(2−3i), we will follow these steps:
Step 1: Expand the first product (4−i)(1+2i)
Using the distributive property (also known as the FOIL method for binomials):
(4−i)(1+2i)=4⋅1+4⋅2i−i⋅1−i⋅2i
Calculating each term:
=4+8i−i−2i2
Step 2: Substitute i2=−1
Since i2=−1, we can replace −2i2 with 2:
=4+8i−i+2
Step 3: Combine like terms
Now, combine the real parts and the imaginary parts:
=(4+2)+(8i−i)=6+7i
Step 4: Expand the second product (1−i)(2−3i)
Using the distributive property again:
(1−i)(2−3i)=1⋅2+1⋅(−3i)−i⋅2−i⋅(−3i)
Calculating each term:
=2−3i−2i+3i2
Step 5: Substitute i2=−1
Replace 3i2 with −3:
=2−3i−2i−3
Step 6: Combine like terms
Now, combine the real parts and the imaginary parts:
=(2−3)+(−3i−2i)=−1−5i
Step 7: Add the results from Step 3 and Step 6
Now, we add the two results together:
(6+7i)+(−1−5i)=(6−1)+(7i−5i)=5+2i
Final Result
The complex number equivalent to the expression is:
5+2i
Step 8: Determine the quadrant
Since the real part 5 is positive and the imaginary part 2 is also positive, the complex number 5+2i lies in the first quadrant.
Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBook:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATHExercise:Grib-In
Explore 32 Videos
- ADDITIONAL TOPICS IN MATH Book:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATH Exercise:PRACTICE TEST
Explore 24 Videos
- COMPLEX NUMBERSBook:ENGLISH SATChapter:COMPLEX NUMBERSExercise:EXERCISE
Explore 6 Videos
Similar Questions
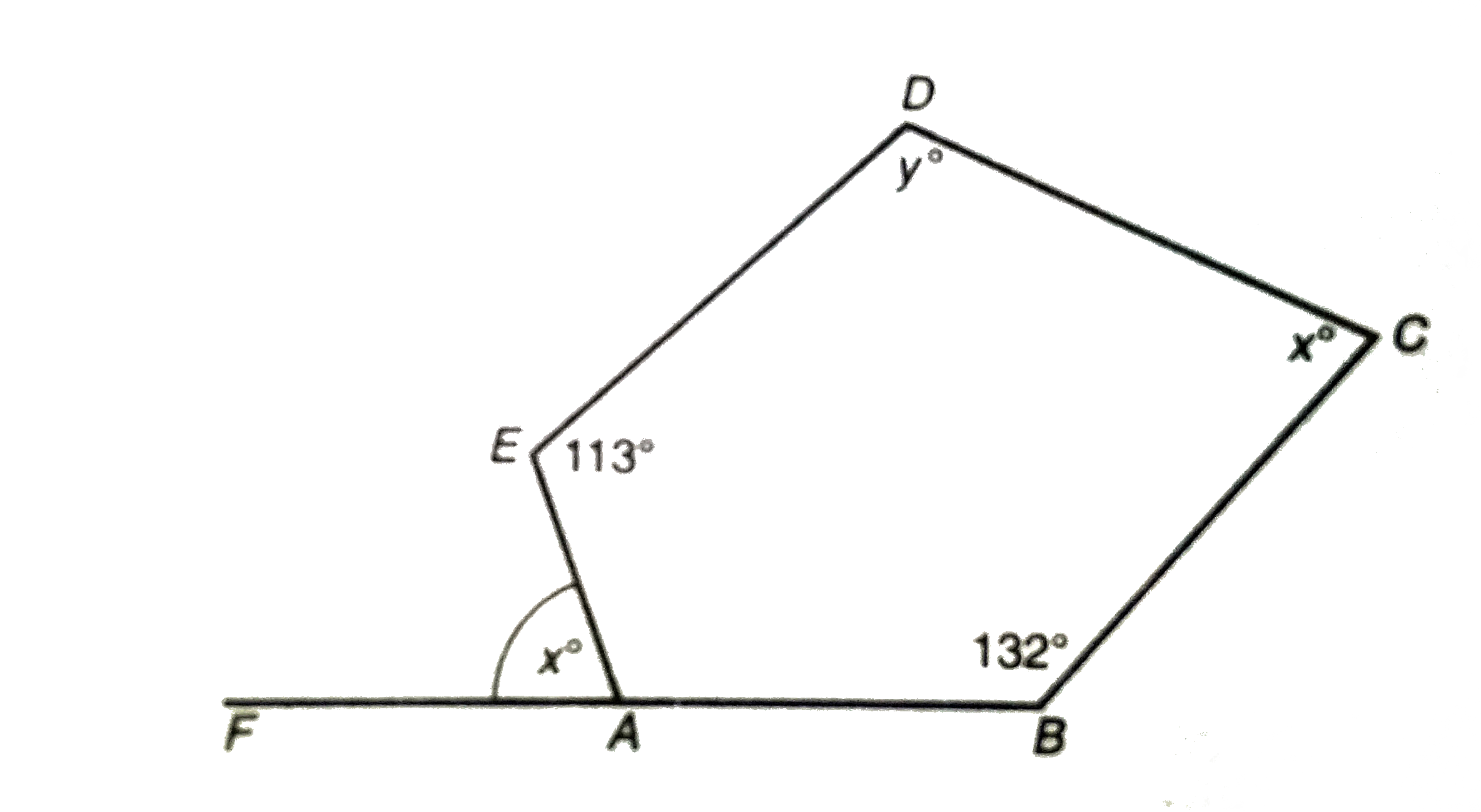
In the accompaying figure of pentagon ABCDE, points F, A, and B lie on the same line. What is the value of y?
View SolutionA rectangular box with length 22 inches , width 5 inches , and height 5 inches is to be packed with steel balls of radius 2 inches in such a way that the centers of the balls are collinear. What is the maximum number of balls that can fit into the box, provided that no balls should protrude from the box ?
View Solutioni29=
View SolutionExpress the following complex number in the polar form: (i) (1+7i)/((2-i)^(2))( ii) (1+3i)/(1-2i)
View SolutionFind the conjugates of the following complex number: (3−2i)(2+3i)(1+2i)(2−i)
View Solution1+2i+3i21−2i+3i2 equals a. i b. -1 c. −i d. 4
View Solutionदी गयी संख्याओं को x+iy के रूप में लिखे ।
(i) z=2+i(1+i)(1−2i) (ii) (1+i)34+3i
View Solutionनिम्नलिखित संख्याओं को ध्रुवीय रूप (polar form) में निरूपित कीजिए ।
(i) 1+7i(2−i)2 (ii) 1+2i1−3i
View Solutionनिम्नलिखित सम्मिश्र संख्याओं के संयुग्मी ज्ञात कीजिए ।
(i) 3+2i (ii) (2+3i)(1−i) (iii) 4−i1+i (iv) (1+i)(2+i)3+i
(v) (3−2i)(3+2i)(1+i) (vi) √2
View SolutionThe imaginary number "I" is such that i2=−1. Which of the following options is equivalent to (1−2i2+3i) ?
View SolutionThe imaginary number I is defined such that i2=−1. Which of the following options is equivalent to (1i+1i2+1i3+1i4) ?
View SolutionIf the correct form of 2i4+4i3−i2+3i is a + ib , where the imaginary number I is such that i2=−1 . What is the value of (a+b) ?
View Solutionनिम्नलिखित सम्मिश्र संख्याओ के संयुग्मी ज्ञात कीजिए :
(a)2+3i (b)3−√3i (c)(1+i)(2−i)
(d)(3+2i)2 (e)1−i1+i (f)3+2i4−3i
View Solutionसम्मिश्र संख्या (1+i)(1+2i)(1+3i) का मापांक ज्ञात कीजिए ।
View SolutionFind the principal argument of the complex number (1+i)5(1+√3i)2−2i(−√3+i)
View Solution
