In body-centered cubic lattice given below, the three distances AB, AC and AA' are
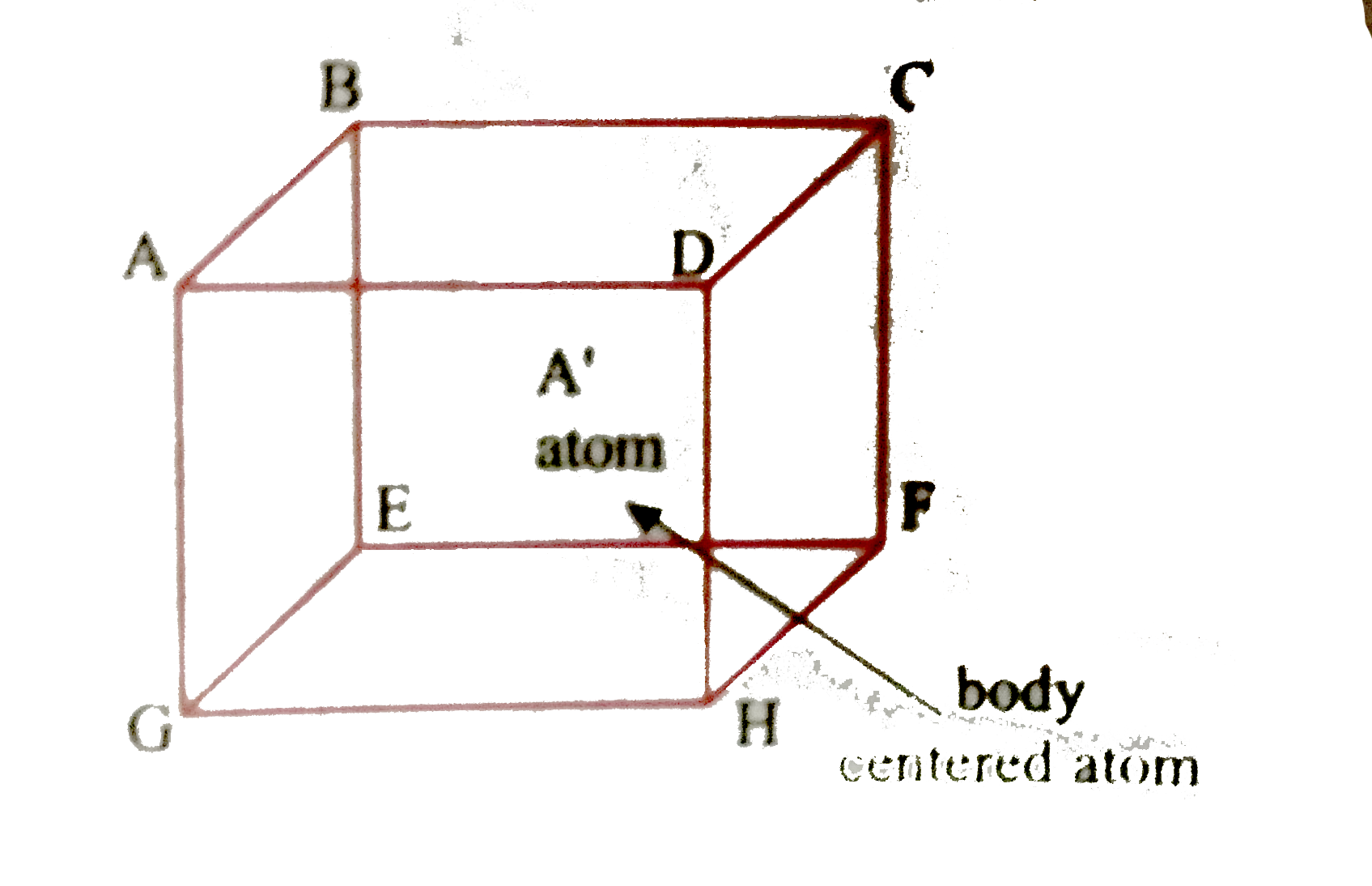
a,√2a,√3a2
a,√3a2,√2a
√3a2,√2a,a
a,a√2,√3a2
i. Edge length =AB=AD=BC=CD=a
ii. AC =√2a
iii. AG (body diagonal) =√3a
Therefore AA=AG/2=√32a
Similar Questions
Body centered cubic lattice has Z=2
View SolutionAmmonium chloride crystallises in a body-centred cubic lattice with a unit distance of 387 pm. Calculate (a) the distance between oppositely charged ions in the lattice and (b) and radius of the NH+4 ion of the radius of Cl− ion is 181 pm.
View Solution
Knowledge Check
In body-centred cubic lattice given below, the three disntances AB,AC, and A' are
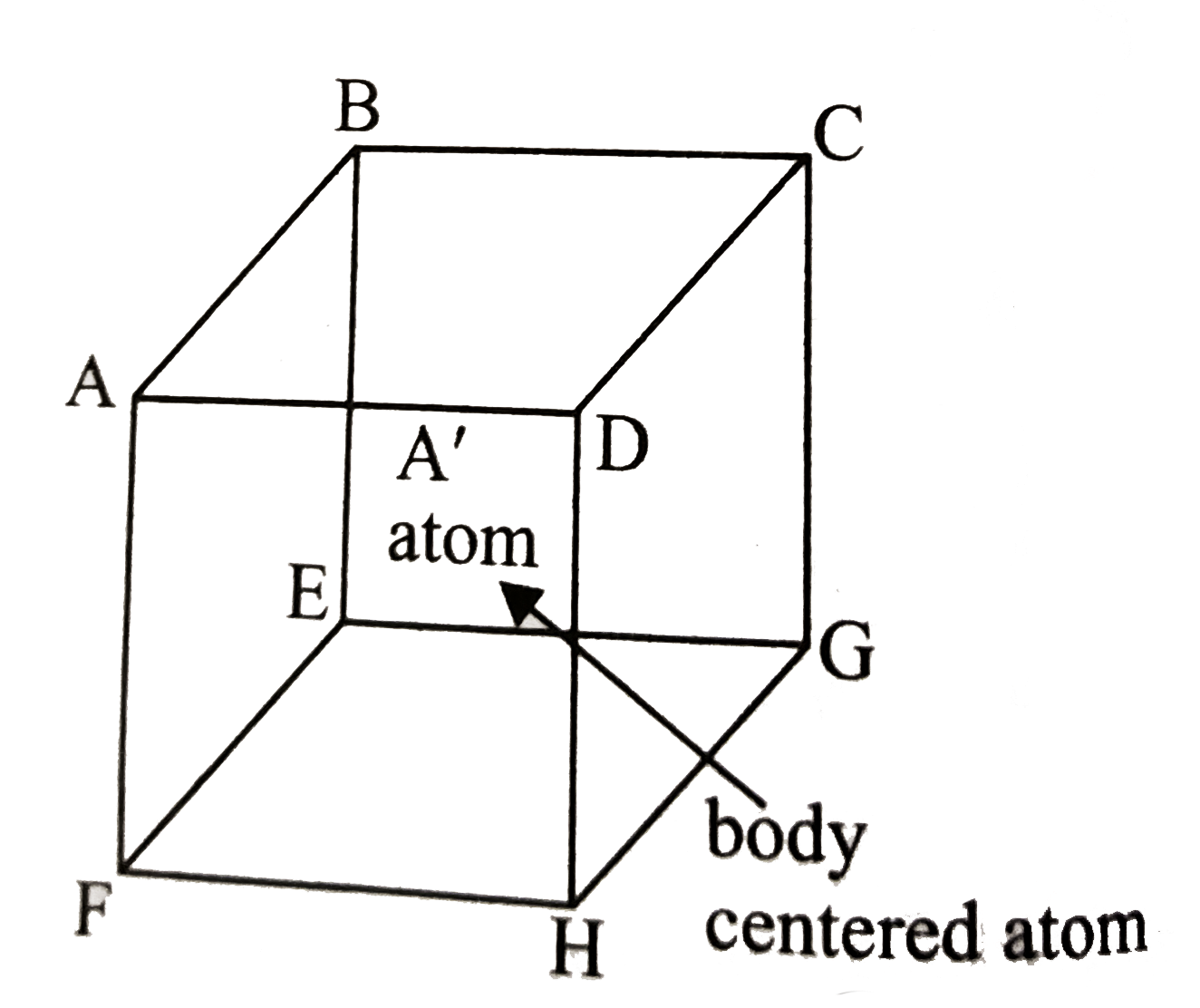 Aa,√2a,√32aBa,√32a,√2aC√32a,√2a,aDa,a√2,√32a
Aa,√2a,√32aBa,√32a,√2aC√32a,√2a,aDa,a√2,√32aIn body-centred cubic lattice given below, the three disntances AB,AC, and ∀' are
 Aa,√2a,√3a2Ba,√3a2,√2aC√3a2,√2a,aDa,a√2a,√3a2
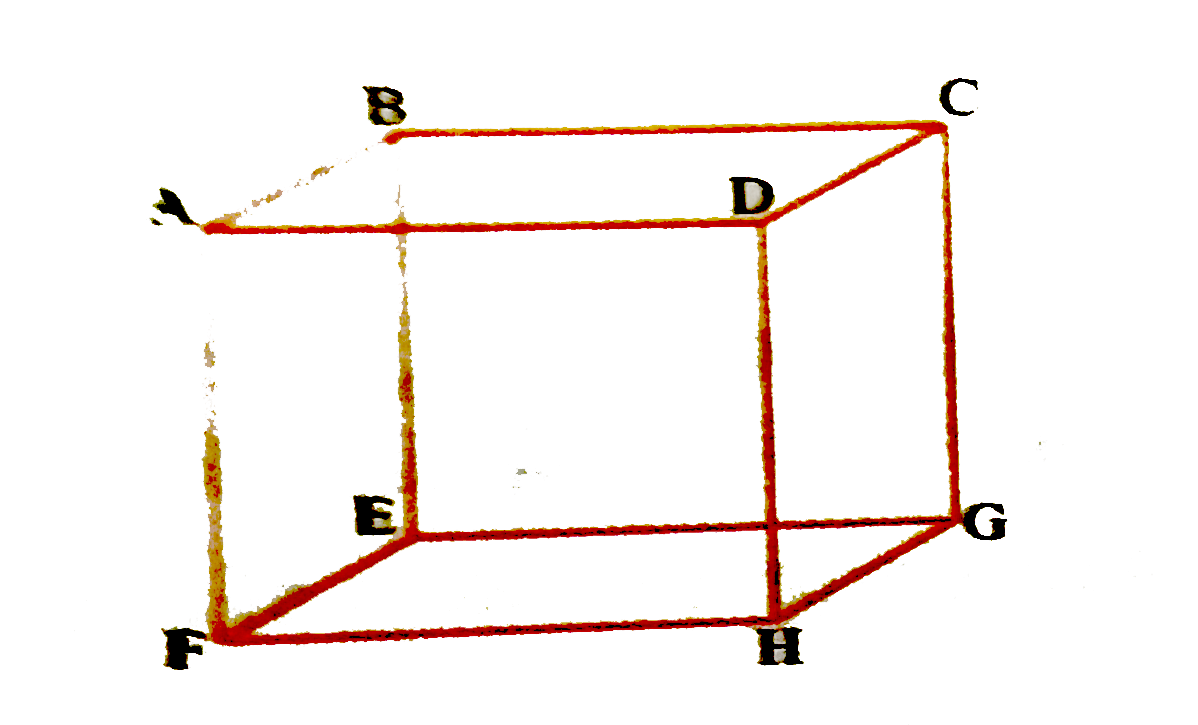
Aa,√2a,√3a2Ba,√3a2,√2aC√3a2,√2a,aDa,a√2a,√3a2In the cubic lattice given below, the three distances between the atoms A−B,A−C, and A−G are, respectively,
 Aa,√2a,√3aBa,√3a,√2aCa2,a√2,√3a2Da,√3a2,√2a
Aa,√2a,√3aBa,√3a,√2aCa2,a√2,√3a2Da,√3a2,√2a
In the cubic lattic given below, the three distances between the atoms A-B,A-C, and A-G are, respectively.
View SolutionIn a body centered unit lattice of A2 type
View SolutionAB crystallises in a body-centred cubic lattice with edge length 'a' equal to 387 pm. The distance between two oppositely charged ions in the lattice is
View SolutionAB crystallizes in a body centred cubic lattice with edge length 'a' equal to 387 pm. The distance between two oppositely charged ions in the lattices is
View SolutionAB crystallizes in a body centred cubic lattice with edge length a equal to 387pm .The distance between two oppositely charged ions in the lattice is :
View Solution
