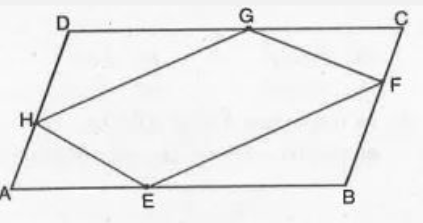
If E,F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar (EFGH) = 12 ar (ABCD)
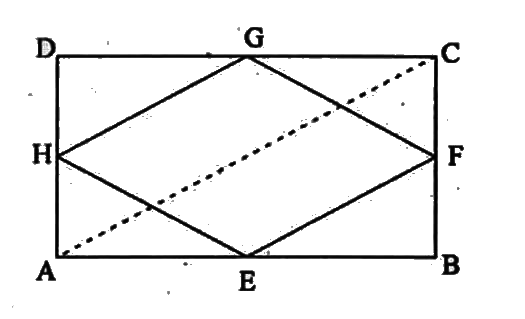 Solution in Kannada
Solution in Kannada
Step by step video & image solution for If E,F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar (EFGH) = (1)/(2) ar (ABCD) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
यदि E, F, G और H क्रमशः समांतर चतुर्भुज ABCD की भुजाओ के मध्य-बिन्दु है, तो दर्शाइए कि (EFGH) 12 ar (ABCD) है।
View Solutionयदि E, F, G और H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं के मध्य-बिन्दु है, तो दर्शाइए कि ar(EFGH)=12ar(ABCD)
View SolutionIf E,F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar (EFGH) = 12 ar (ABCD)

View SolutionIf E, F G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar(EFGH) =12 ar (ABCD) .
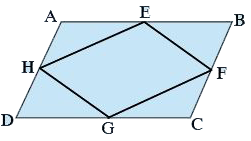
View SolutionIf E, F G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar(EFGH) =12 ar (ABCD) .
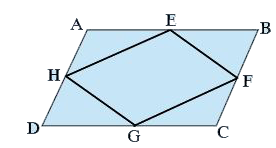
View SolutionIf E, F G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar(EFGH) =12 ar (ABCD) .
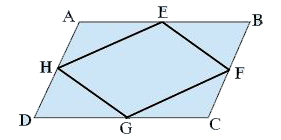
View SolutionIf E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH)=12ar(ABCD).
View SolutionIf E, F, G and H are the mid-points of sides of a parallelogram ABCD then ar (EFGH) = ............ .
View Solution
