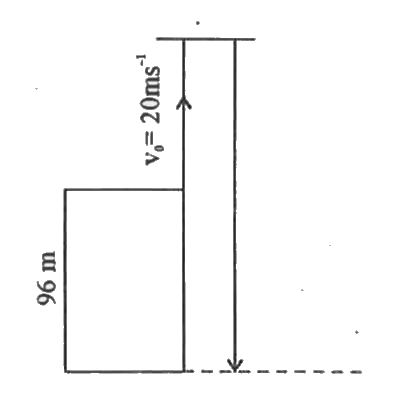
A stone is thrown vertically upwards with a velocity of 20ms−1 from the top of a tower 96 m high. After what time will it reach the foot of the tower ? What will be the velocity of the stone reaching the point of projection? At what velocity will it strike the ground ? (g=9.8ms−2)Solution in Kannada
Given v0=20ms−1,g=9.8ms−2.
using h = 96 m
h=v0t+1/2gt2 where
h=−h,g=−g we get
−96=20t−t/2×9.8t2
−4.9t2−20t+96=0
or 4.9t2−20t−96=0
∴ t=20±√480+1881.62×4.9=20±47.779.8
i.e. t=67.779.8=6.91s
Velocity of the stone reaching the point of projection =−20ms−1
By applying the formula v2=v20+2ax
we get v2=v20+2(−g)(−h)=(20)2+2×9.8×96=2281.6
∴ v=47.77ms−1
Similar Questions
A stone projected vertically up with velocity v from the top of a tower reaches the ground with velocity 2v.The height of the tower is
View SolutionA stone is thrown upwards with initial velocity 'u' from top of a tower and it reaches to ground with velocity '3u' then height of the tower is ......
View SolutionA stone projected vertically up with velocity v from the top of a tower reaches the ground with velocity 2v. The height of the tower is
View SolutionA stone is projected vertically upward from the top of a tower with a velocity u and strikes the bottom of the tower with a velocity 3u. The distance travelled by the stone is
View SolutionA stone projected vertically up with velocity v from the top of a tower reaches the ground with velocity 2v. The height of the tower is
View SolutionA stone is projected vertically upward from the top of a tower with a velocity u and strikes the bottom of the tower with a velocity 3u. The distance travelled by the stone is
View SolutionA stone projected vertically up with velocity v from the top of a tower reaches the ground with velocity 2v. The height of the tower is
View SolutionA stone is thrown upwards with a speed u from the top of a tower reaches the ground with a velocity 3 u . The height of the tower is
View Solution

