Show that a=v2r and hence obtain an expression for centripetal force.Solution in Kannada
Let →r and →r, be the position vectors and →v velocities of the object when it is it point P and P. By definition, velocity at a point is along the tangent at that point in the direction of the motion. Since the path is circular, →v is perpendicular to →r and →v is perpendicular to →r
Therefore, △→v is perpendicular to △→r. Average acceleration △→v△t is perpendicular to △→r
The magnitude of →a is, by definition, given by |→a|=lim△t→0△→v△t
The triangle formed by the position vectors is similarly to the triangle formed by the velocity vectors.
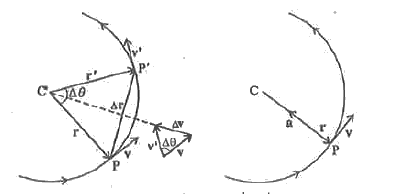
i.e, |△→v|v=|△→r|r or |△→v|=v(|△→r|)r
Therefore, |→a|=lim∣△→v△t=lim△t→0v|△→r|r△t=→vrlim△t→0|△→r|△t
If △t is very small, △θ will also small. The arc PP' is approximately equal to |△→r|
i.e., lim△t→0|△→r|△t=v Thus, centripetal acceleration |→a|=vfv=v2r and →a=vrd→rdt
The centripetal acceleration is always directed towards the centre. The centripetal force=ma.
Similar Questions
The centripetal force on a body of mass 'm' and velocity 'v' moving in circular orbit of radius 'r' is given by F = mv2r. Using the formula of centripetal force write an quation to find percentage error in centripetal force.
View SolutionDefine centripetal force. Derive an expression for it.
View SolutionWhat is centripetal force? Derive an expression for it. Show that centripetal force does no work.
View SolutionObtain an expression for the centripetal force required to make a body of mass m moving with a constant speed v around a circular path of radius r.
View SolutionWrite an expression for the centripetal force.
View SolutionDefine centripetal force and find an expression for it.
View SolutionA body of mass m moves in a circular path of radius r with a velocity v. Find the expression for the centripetal force F acting on the body by using method of dimensions.
View SolutionUsing the dimensional equation, show that the centripetal force = (mv^(2))/(r)
View Solution

