Let x1,x2,x3 be the points where f(x)=|1−|x−4∣∣,x∈R is not differentiable then f(x1)+f(x2)+f(x3)=
Video Solution
Text Solution
The correct Answer is:1
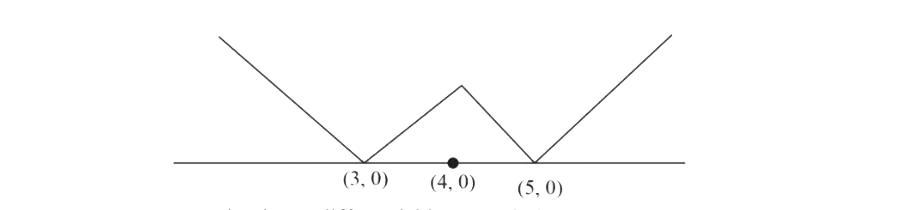
Function is not differentiable at x=3,4,5
So,f(3)+f(4)+f(5)
0+1+0=1
|
Similar Questions
Knowledge Check
Let f(x)=||x|−1|, then points where, f(x) is not differentiable is/are
A0,±1B±1C0D1Let f(x)=||x−1|−1|, then all the points where f(x) is not differentiable is (are)
A1B1, 2C±1D0, 1, 2If f(x)=||x|-1|, then points, where f(x) is not differentiable, is/(are)
A0,±1B±1C0D1
Let f(x)=||x|−1|, then points where, f(x) is not differentiable is/are
View SolutionIf f(x)={x3,x2<1andx,x2≥1 then f(x) is differentiable at
View SolutionIf f(x)=[[x3,|x|<1],[x,|x|≥1], then number of points where f(x) is non-differentiable is
View SolutionLet f(x)= max{4,1+x2,x2−1}∀x∈R. Total number of points, where f (x) is non-differentiable, is equal to
View SolutionThe number of points of f(x)=|x-1|+|x-3|+sinx, x in [0,4), where f(x) is not differentiable, is
View Solution
