In an experiment for measuring 'g', a body is thrown vertically up in an evacuated tube and allowed to come back. If ΔTL is the time interval between the two passages of the object across a lower level and ΔTH the time interval between two passages across an upper level and H the distance between two levels as shown in Fig. 5.70 show that:
g=8HΔT2L−ΔT2H
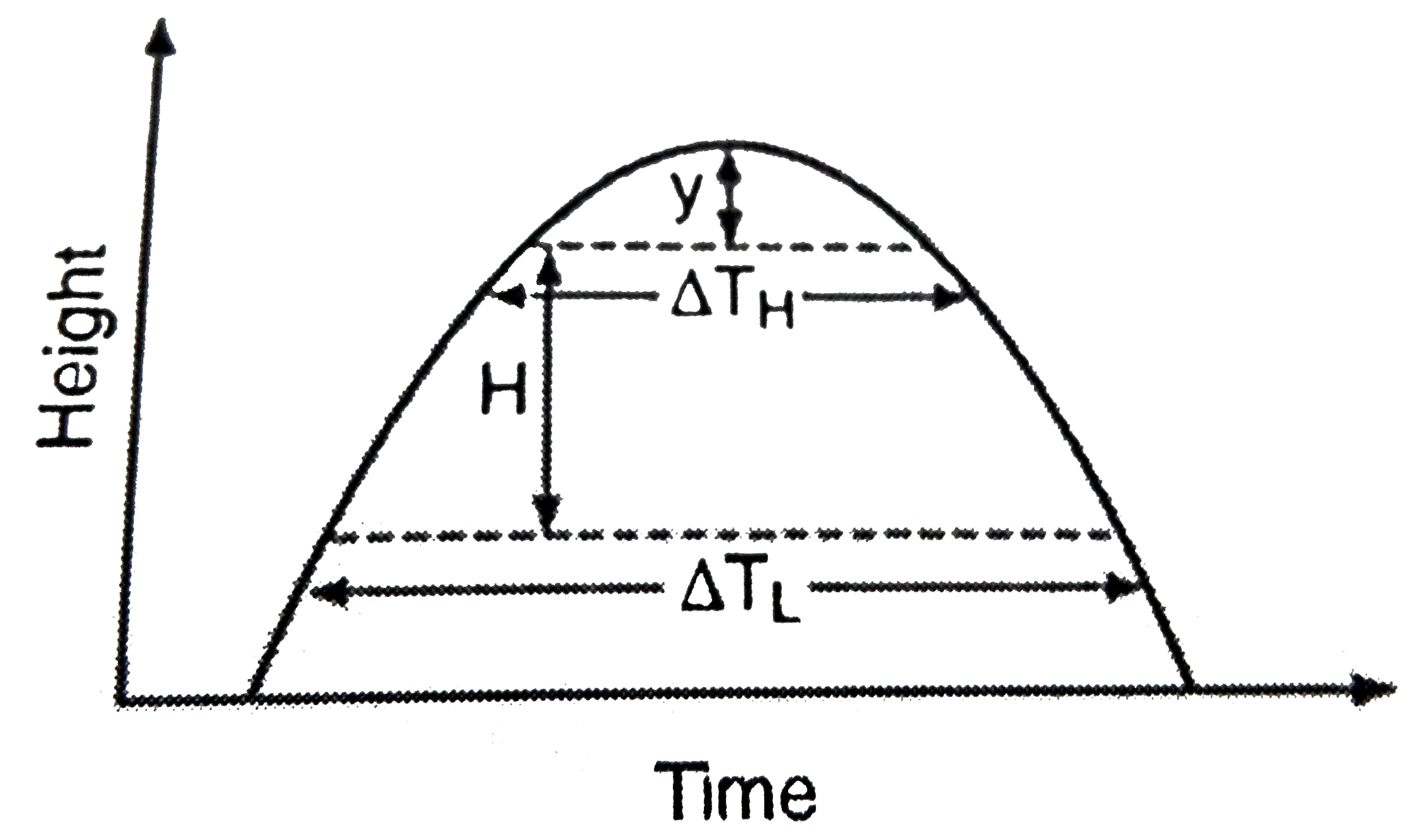
Time taken by a body to go up and come down a height h is giving by t=2, √(2h/g)√(8h/g). So , if y is the height of highest point above higher level, time taken to go up and come down ΔTH=√(8y/g) while for lower level
ΔTL=√[8(y+h)/g].
∴ΔT2L−ΔT2H=8(y+H)g−8yg=8Hg
or g=8H(ΔT2L−ΔT2H)
Topper's Solved these Questions
Similar Questions
A particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (1):
View SolutionIf force, mass and time are taken to be base physical quantities with dimensional formula [F], [M] and [T], then :
Dimensional formula for energy is :
View Solution1g of a non-volatile non-electrolyte solute is dissolved in 100g of two different solvents A and B whose ebullioscopic constants are in the ratio of 1 : 5. The ratio of the elevation in their boiling points, (DeltaT_(b)(A))/(DeltaT_(b)(B)) is
View SolutionTwo intervals of time are measured as Delta t_(1) = (2.00 pm 0.02) s and Delta t_(2) (4.00pm 0.02)s . The value of sqrt( ( Deltat_(1)) ( Deltat_(2))) with correct significant figures and error is
View SolutionIf DeltaT_(f) is the depression in freezing point for the electrolyte and DeltaT_(f)^(@) for the non-electrolyte of the same concentration, then Van't Hoff factor (i) is
View SolutionConsider equimolal aqueous solutions of NaHSO_(4) and Nacl with Delta T_(b) and DeltaT_(b)^(1) as their respective boiling point elevations. The value of underset (xrarrinfty)(Lt) (DeltaT_(b))/(DeltaT_(b)) will be
View SolutionThe factor (ΔTf/Kf) represents
View SolutionHow are DeltaT_(b) and DeltaT_(f) related to the molar mass of the solute?
View Solution
