On applying a force F the mass M is displaced vertically down by from equilibrium position, Find the force F in terms of the force constant k of the spring and displacement y for the cases (A) and (B) as shown in
Case (A) for the equilibrium of mass M
F=T …(i)
and for the equilibrium of pulley
2T=F' …(ii)
But as due to shift of mass M by y, the spring strentches by (y/2) so
F'=k(y/2) ….(iii)
So, substituting F' from Eqn. (iii) in Eqn. (ii) and then T from Eqn (ii) in Eqn. (i) we get
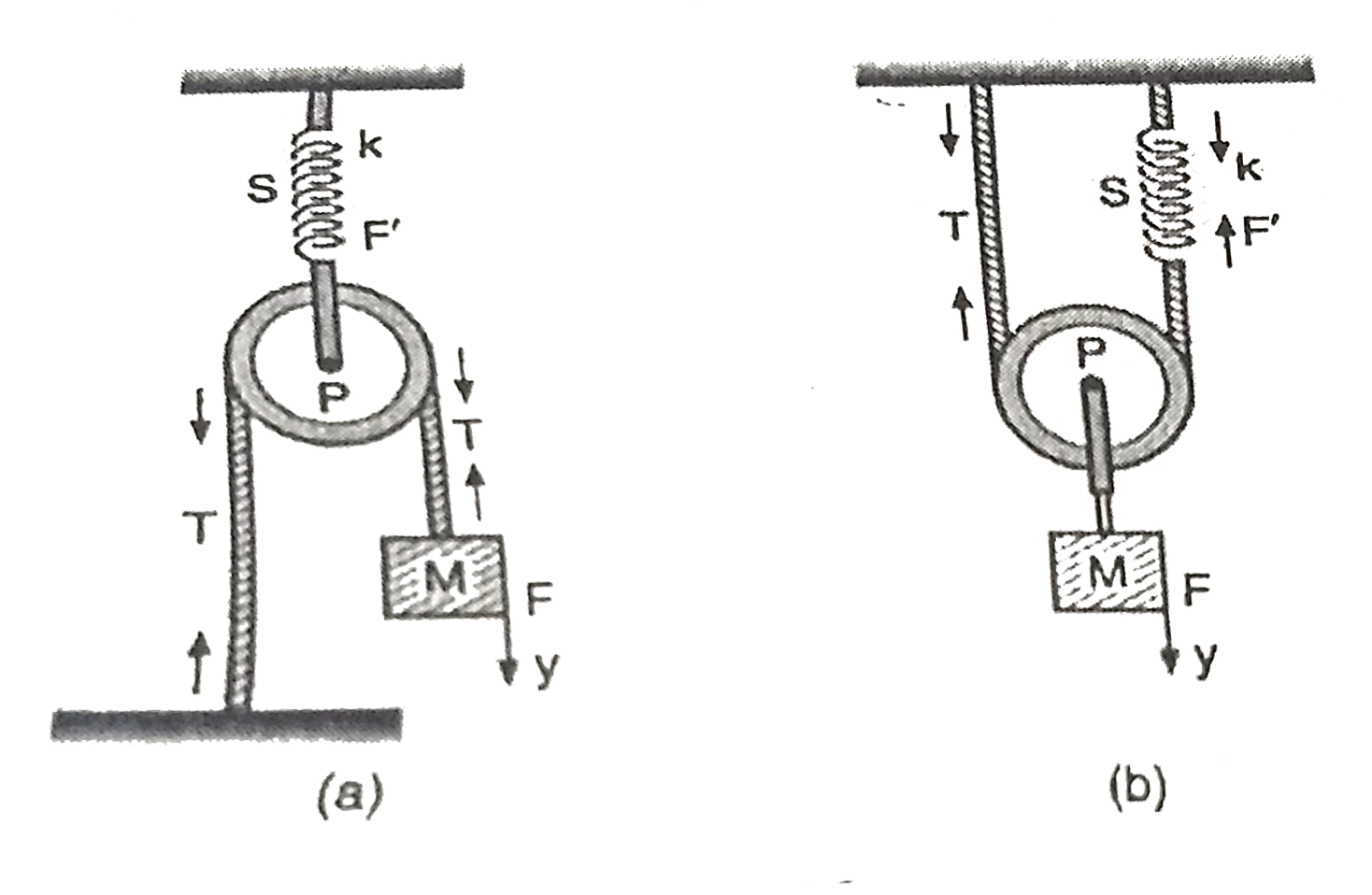
Case (B) As tension in massless string and spring will be same,
T=F'
And for equilibrium of pulley T+F'=F ...(i)
So, from Eqns (i) and (ii) F=2F' ....(ii)
Now if the mass M shifts by y the spring will stretch by 2y (as string is inextensible)
F'=k(2y) ....(iv)
So, subsituting f' from Eqn (iv) in Eqn (iii)
F=(4k)y ...(b)
Topper's Solved these Questions
Similar Questions

When F = 2 N , the frictional force between 5 kg block and ground is :
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionThe force constant between the restoring force F and displacement x of a spring accoring to the graph shown will be
View SolutionThe potential energy of a spring pendulum, with a mass m connected to it, is given by V=1/2kx^(2) (where x = displacement from the position of equilibrium and k = a constant). How does the applied force on the mass vary with displacement?
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionThe valuve of force constant between the applied elastic force F and displacement with be
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View Solution

