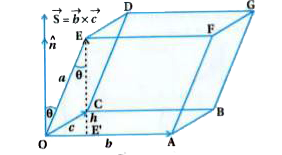
Show that →a.(→b×→c) is equal in magnitude to the volume of the parallelpiped formed by the vectors →a,→band→c
Let a parallelopiped be formed on the three vectors −−→OA=→a,−−→OB=→b
and −−→OC=→cNow, →b×→c=bcsin90∘ˆn=bcˆn
where ˆn is unit vector along −−→OA perpendicular to the plane containing →b and →c.
Now →a(→b×→c)=→a. bcˆn
which is equal in magnitude to the volume of the parallelpiped.

Similar Questions
vecA+vecB+vec C=0 If so, show that, vecA×vecB=vecB×vec C=vec C×vecA
View SolutionIf (→A+→B)⋅(→A−→B)=0 , show that the magnitude of both the vectors are equal .
View Solution→a,→b,→c are three vectors with magnitude |→a|=4,∣∣→b∣∣=4,|→c|=2 and such that →a is perpendicular to (→b+→c),→b is perpendicular to(→c+→a) and →c is perpendicualr to (→a+→b) . It follows that ∣∣→a+→b+→c∣∣ is equal to :
View SolutionShow that veca.(vecbxxvec c) is equal in magnitude to the volume of the parallelpiped formed by the vectors veca,vecb and vec c
View SolutionVolume of parallelpiped formed by vectors →a×→b,→b×→cand→c×→a is 36 sq. units.

View SolutionShow that →a.(→b×→c) is equal in magnitude to the volume of the parallelopiped formed on the three vectors, →a,→band→c
View SolutionThe scalar triple product [→a+→b−→c →b+→c−→a →c+→a−→b] is equal to :
View SolutionIf veca,vecb,vec(c) are non-coplanar, then show that the vectors veca-vecb,vecb+vec(c),vec(c)+vec(a) are planar.
View Solution

