The function g is defined by g(x)=2x2−dx−6, where d is a constant. If one of the zeros of g is 6, what is the value of the other zero of g?
2
12
−12
-2
The correct Answer is:C
To solve the problem, we need to find the other zero of the function g(x)=2x2−dx−6 given that one of the zeros is x=6.
1. Substitute the known zero into the function: Since g(6)=0, we can substitute x=6 into the function to find d.
g(6)=2(62)−d(6)−6=0
This simplifies to:
2(36)−6d−6=0
72−6d−6=0
66−6d=0
2. Solve for d: Rearranging the equation gives:
6d=66
Dividing both sides by 6:
d=11
3. Substitute d back into the function: Now that we have d, we can rewrite the function:
g(x)=2x2−11x−6
4. Use the quadratic formula to find the zeros: The quadratic formula is given by:
x=−b±√b2−4ac2a
Here, a=2, b=−11, and c=−6.
5. Calculate the discriminant:
b2−4ac=(−11)2−4(2)(−6)=121+48=169
6. Substitute values into the quadratic formula:
x=−(−11)±√1692(2)=11±134
7. Calculate the two possible values for x:
- First zero:
x1=11+134=244=6
- Second zero:
x2=11−134=−24=−12
8. Conclusion: The other zero of the function g(x) is:
−12
Final Answer:
The value of the other zero of g is −12.
g(6)=2(62)−d(6)−6=0
This simplifies to:
2(36)−6d−6=0
72−6d−6=0
66−6d=0
6d=66
Dividing both sides by 6:
d=11
g(x)=2x2−11x−6
x=−b±√b2−4ac2a
Here, a=2, b=−11, and c=−6.
b2−4ac=(−11)2−4(2)(−6)=121+48=169
x=−(−11)±√1692(2)=11±134
- First zero:
x1=11+134=244=6
- Second zero:
x2=11−134=−24=−12
−12
The value of the other zero of g is −12.
Similar Questions
g(x)=a√41−x2
Function g is defined by the equation above where a is a nonzero real constant. If g(2i)=√5, where i=√−1, what is the value of a?
View Solutiong(x)=x4−kx3+13x2−12x+4
The function g is defined above, and k is a constant. In the xy- plane, the graph of g intersects the y - axis at (0,4) and intersects the x - axis at (1,0) and (2,0). What is the value of k?
View Solution
Knowledge Check
IF the function g is defined by g(x)=3x+5, what is the value of g(-5)?
A-20B-10C20D60A function g(x) is defined as g(x)=−5x2. What is g(−2)?
A−100B−20C20D50If function g is defined by g(x)=x-1 and 2g(c)=10, what is the value of g(3c)?
A6B9C15D17
If g(x)=3x+√x, what is the value of g(d2+6d+9) ?
View Solution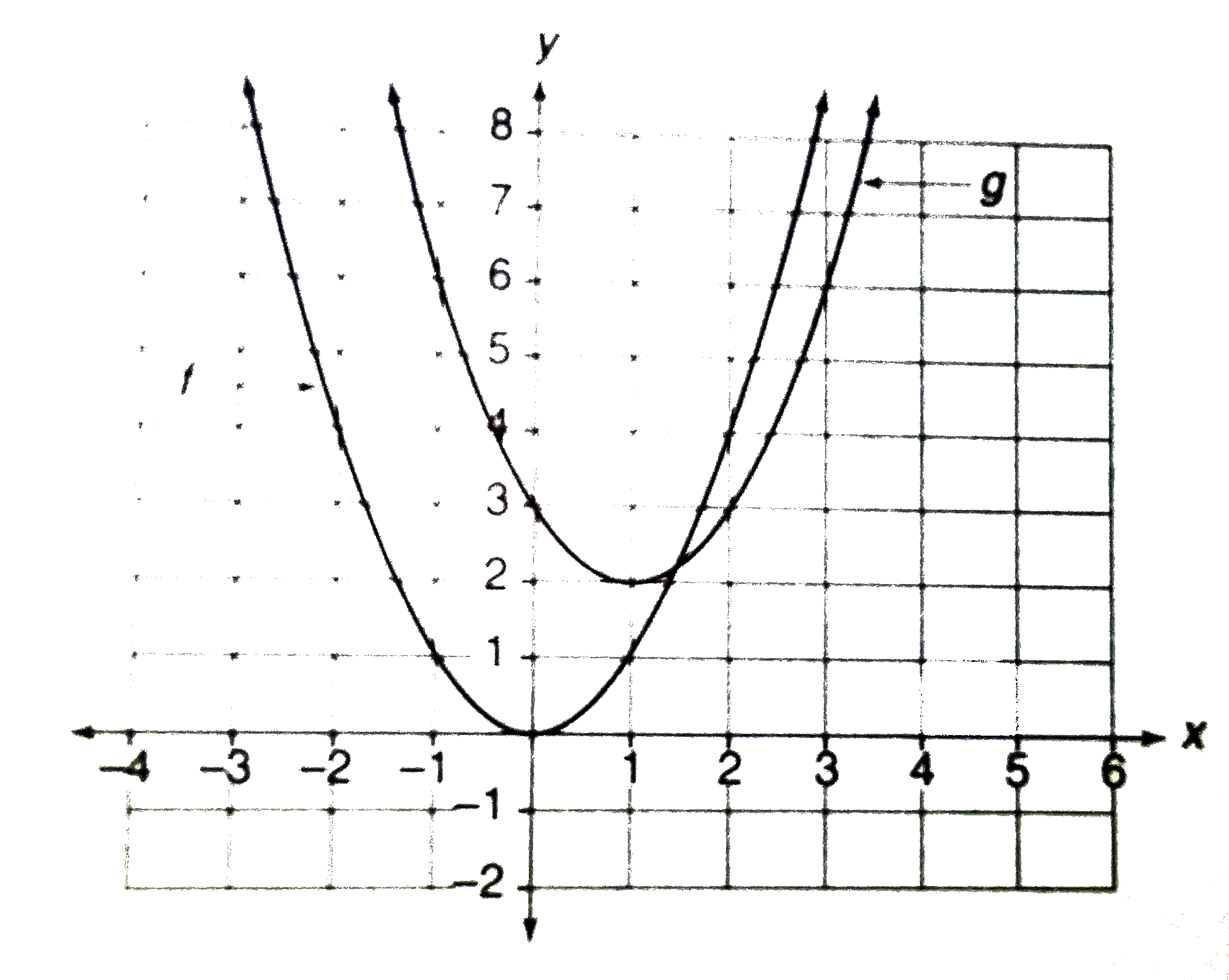
The accompanying figure shows the graphs of functions f and g. If f is defined by f(x)=x2 and g is defined by g(x)=f(x+h)+k, where h and k are constants, what is the value of h+k?
View SolutionThe functions r is defined as g(x)=x23−|x−4|. For which values of x is g(x) NOT defined?
View SolutionThe function g is defined above. What is the value of g(−4x) ?
View SolutionLet the function g be defined by g(x)=5x+2. If √g(a2)=6, what is the value of a?
View Solution
