किसी टावर के पाद से 160 मी . दूर स्थित बिंदु से टावर का उन्नयन कोंढ टावर के पाद की ओर 100 मी . दूरी चलने पर दो गुना हो जाता है । टावर की ऊंचाई ज्ञात करे ।
80 m
100 m
160 m
200 m
The correct Answer is:A
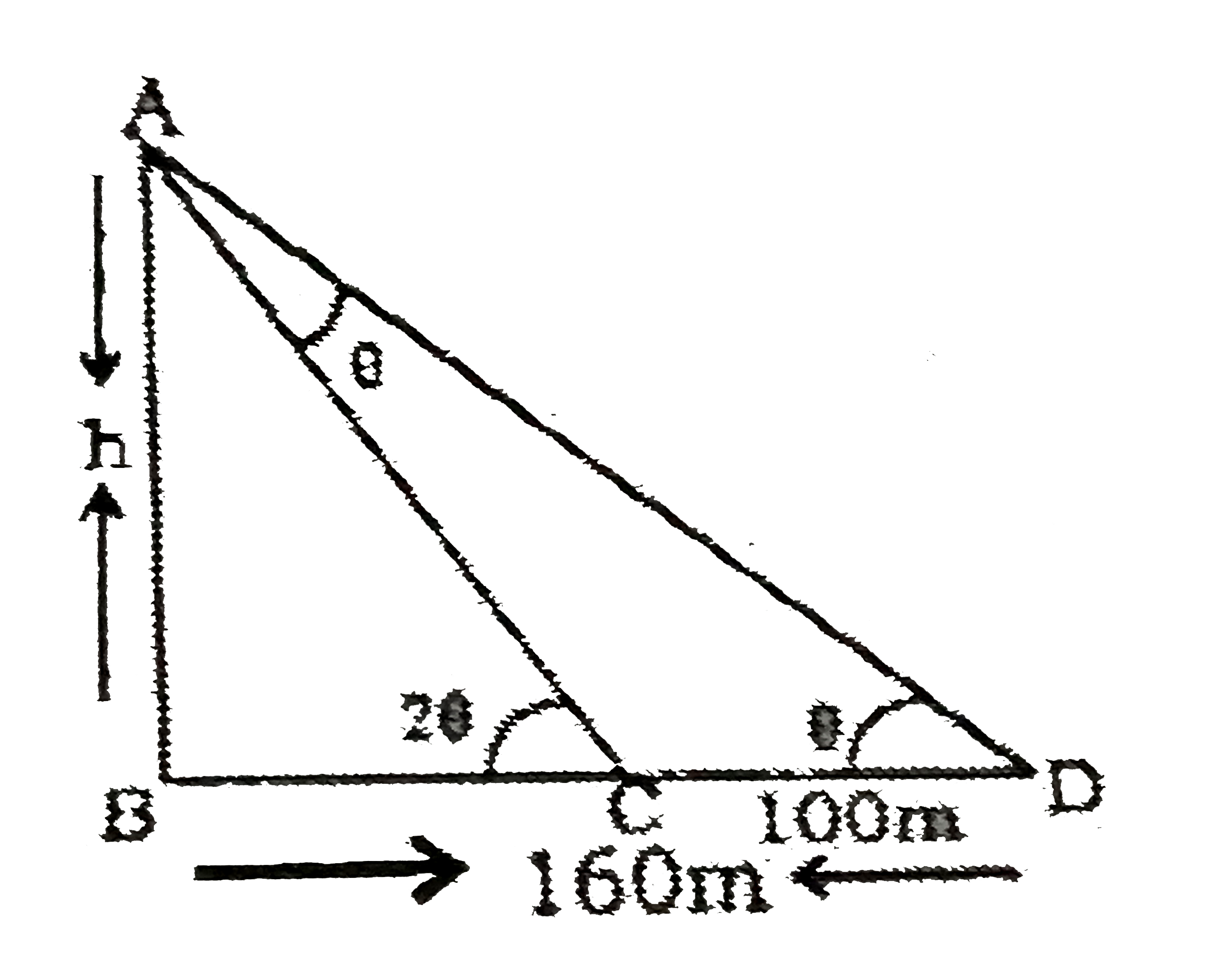
BD=160m
In △ACD
exter. ∠ACB=∠CAD+∠ADC
2θ=∠CAD+θ
∠CAD=θ
∴AC=CD
AC=100 m
In △ABC
AC=100 m
BC=160-100 =60 m
Then AB=80 m (By pythagoras theorem)
Similar Questions
बिंदु P की बिंदु (4,3) से दूरी √10 है। बिंदु P के निर्देशांक ज्ञात कीजिए यदि इस की कोटि भुज से दुगुनी हो।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View Solutionसरल रेखाएँ|एक बिन्दु की रेखा से दूरी#!#दो समांतर रेखाओ के बीच की दूरी#!#प्रश्नो पर चर्चा
View Solutionबिंदु L बिंदु P(3,4,5) से xz तल पर खींचे गए लंब का पाद बिंदु है | बिंदु L के निर्देशांक है
View SolutionFrom a point P, the angle of elevation of a tower is such that its tangent is 3/4. On walking 560 meters towards the tower the tangent of the angle of the elevation of the tower becomes 4/3. What is the height (in meters) of the tower?
एक बिंदु P से, एक टावर की ऊँचाई का कोण ऐसा है कि इसकी स्पर्शरेखा 3/4 है। टॉवर को ओर 560 मीटर चलने पर टॉवर के ऊंचाई के कोण के स्पर्शरेखा 4/3 हो जाती है। मीनार की ऊँचाई (मीटर में) कितनी है?
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View SolutionThe shadow of a tower, when the angle of elevation of the sun is 60^@ is found to be 15 m shorter than when it is 45^@ . Then height of the tower is जब सूर्य का उन्नयन कोण 60^@ है तो एक टावर की परछाईं इसके 45^@ होने की तुलना में 15 मीटर छोटी पायी जाती है | इस टावर की ऊंचाई क्या है?
View Solution