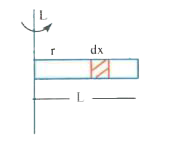
A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
The correct Answer is:T=mω2wl(l2−x2)
Choose a small element of width dx at a distance x from one end of the rod . The mass of the element = dmml dx . Let T is the tension in the rod at a distance x . By Newton's second law for the motion of element of mass dm we have
T−(T+dT)=(dm)ω2x
or −dT=(mldx)ω2x
Integrating above equation , we get
−∫0TdT=mω2l∫lxxdx
or −|T|0T=mω22l∣∣x2∣∣lx lt brgt or −(0−T)=mω22l(l2−x2)
or T=mω22l(l2−x2)
At x = 0 , T = Tmax=mω2l2
At x = l2,T=mω2l8
Topper's Solved these Questions
Similar Questions

When F = 2 N , the frictional force between 5 kg block and ground is :
View SolutionA particle is moving along X-axis under a force such that its position -time graph is as shown in figure.

As the particle passes position (1):
View Solutionद्रव्यमान M व लम्बाई L की पतली छड़ की घूर्णन त्रिज्या छड़ की लम्बाई के लम्बवत् तथा छड़ के एक सिरे से गुजरने वाले अक्ष के परितः ज्ञात कीजिये।
View SolutionA thin uniform rod of length L and radius r rotates with an angular velocity in a horizontal plane about a vertical axis passing through one of its ends. The density of the material is ρ and Youngs modulus is Y. 1) Find tension in the rod at distance Y from the axis. 2) Find elongation of the rod
View SolutionA uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity \(omega\) in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity omega about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View SolutionA uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B . The rod begins rotating from rest. The angular velocity omega at angle theta is given as
View Solution

