At the endpoint and midpoint of a circular are AB, tangent lines are drawn, and the points, A and B are jointed with a chord. Prove that the ratio of the areas of the triangles thus formed tends to 4 as the arc AB decreases infinitely.
The correct Answer is:4
Step by step video, text & image solution for At the endpoint and midpoint of a circular are AB, tangent lines are drawn, and the points, A and B are jointed with a chord. Prove that the ratio of the areas of the triangles thus formed tends to 4 as the arc AB decreases infinitely. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITBOOK - MOTIONCHAPTER - LIMITEXERCISE - EXERCISE-4
17 Videos
- LIMITBOOK - MOTIONCHAPTER - LIMITEXERCISE - EXERCISE-2(LEVEL-2)
5 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - MOTIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise -4 Level -II
7 Videos
- MATRICES BOOK - MOTIONCHAPTER - MATRICES EXERCISE - Exercise - 4 (Level-II)
28 Videos
Similar Questions
Let α and β be the distinct roots of ax2+bx+c=0 then Ltx→α1−cos(ax2+bx+c)(x−α)2 equal to
View SolutionLet f(x)=cos2−cos2xx2−|x| , then
View SolutionIf 0<x<1, then √1+x2[{xcos(cot−1x)+sin(cot−1x)}2−1]1/2 is equal to
View SolutionLet A=[1000110−24],I=[100010001]andA−1=[16(A2+cA+dI)]. Then value of candd are a.(=6,−11) b. (6,11) c. (−6,11) d. (6,−11)
View SolutionAt the endpoint and midpoint of a circular are AB, tangent lines are drawn, and the points, A and B are jointed with a chord. Prove that the ratio of the areas of the triangles thus formed tends to 4 as the arc AB decreases infinitely.
View SolutionLet (a, b) is the midpoint of the chord AB of the circle x^2 + y^2 = r^2. The tangents at A and B meet at C, then the area of triangle ABC
View SolutionPoints A and B are on a circle of radius 5 and AB=6. Point C is the midpoint of the minor arc AB length of the line segement AC, is:
View SolutionAB is a chord of the circle x^(2)+y^(2)=9 .The tangents at A and B intersect at C. If M(1,2) is the midpoint of AB,then the area of triangle ABC is
View Solutionसिद्ध कीजिए कि वृत्त के किसी चाप के मध्य बिन्दु पर खींची गई स्पर्श रेखा, चाप के अन्तः बिन्दुओं को मिलाने वाली जीवा के समान्तर होती हैं।
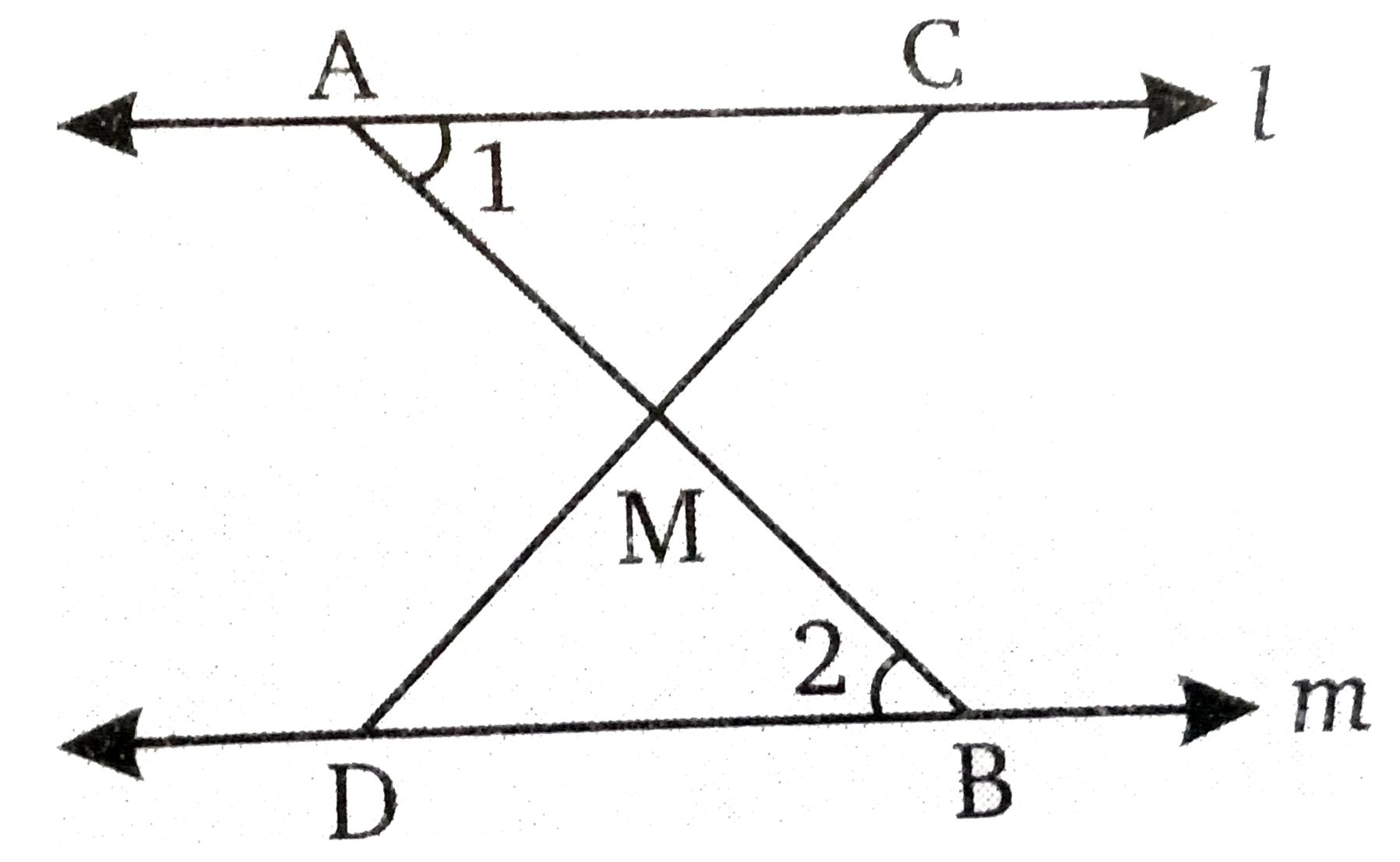
View Solutionचित्र में l∣∣m तथा M, रेखाखण्ड AB का मध्य बिंदु है । सिद्ध कीजिए कि M, एक रेखाखण्ड CD, जिसके अन्तः बिंदु l व mपर स्थित है , का भी मध्य बिंदु है ।
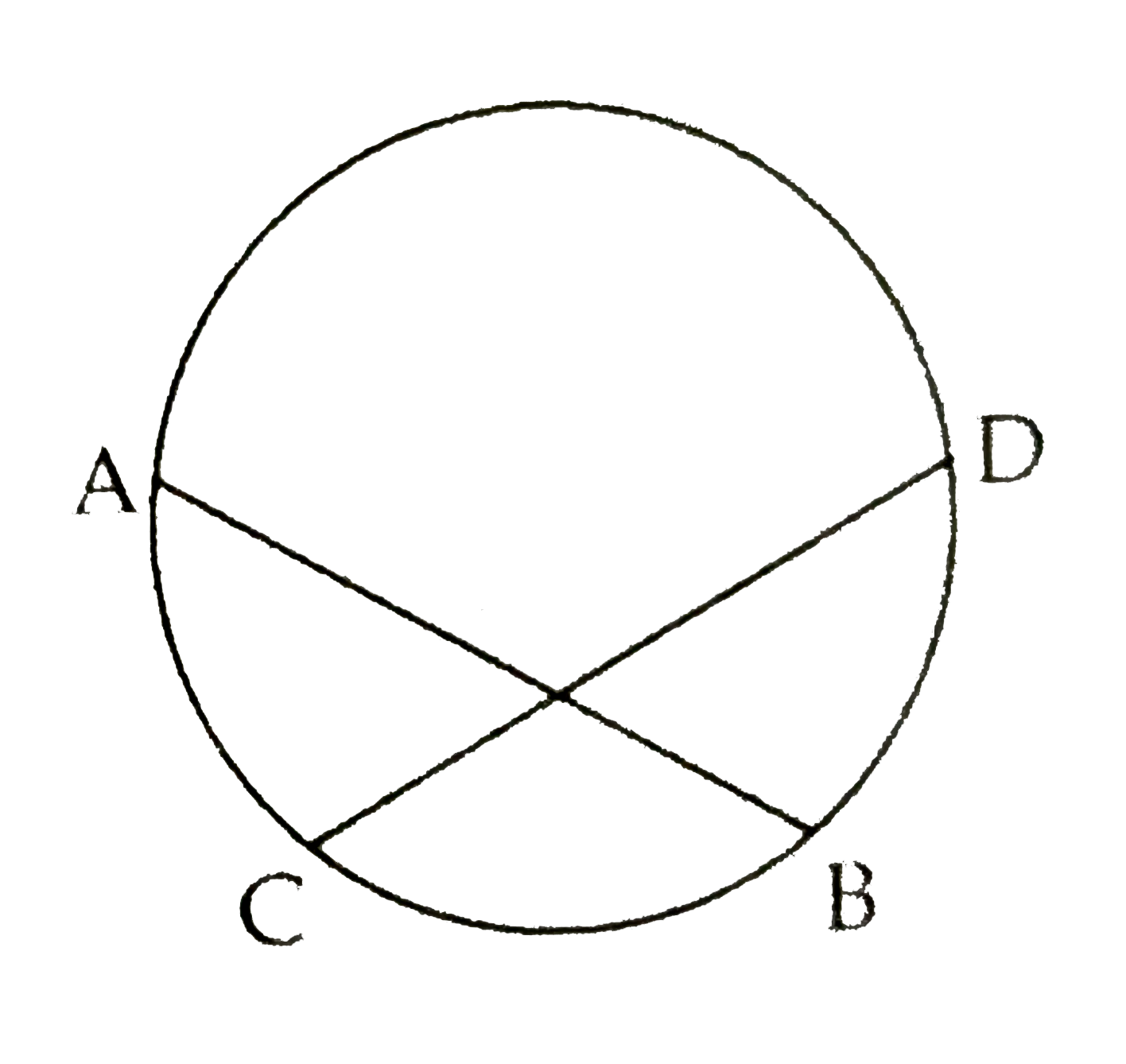
View SolutionIn the adjoining figure, chord AB ≅ chord CD . Prove that arc AC ≅ BD
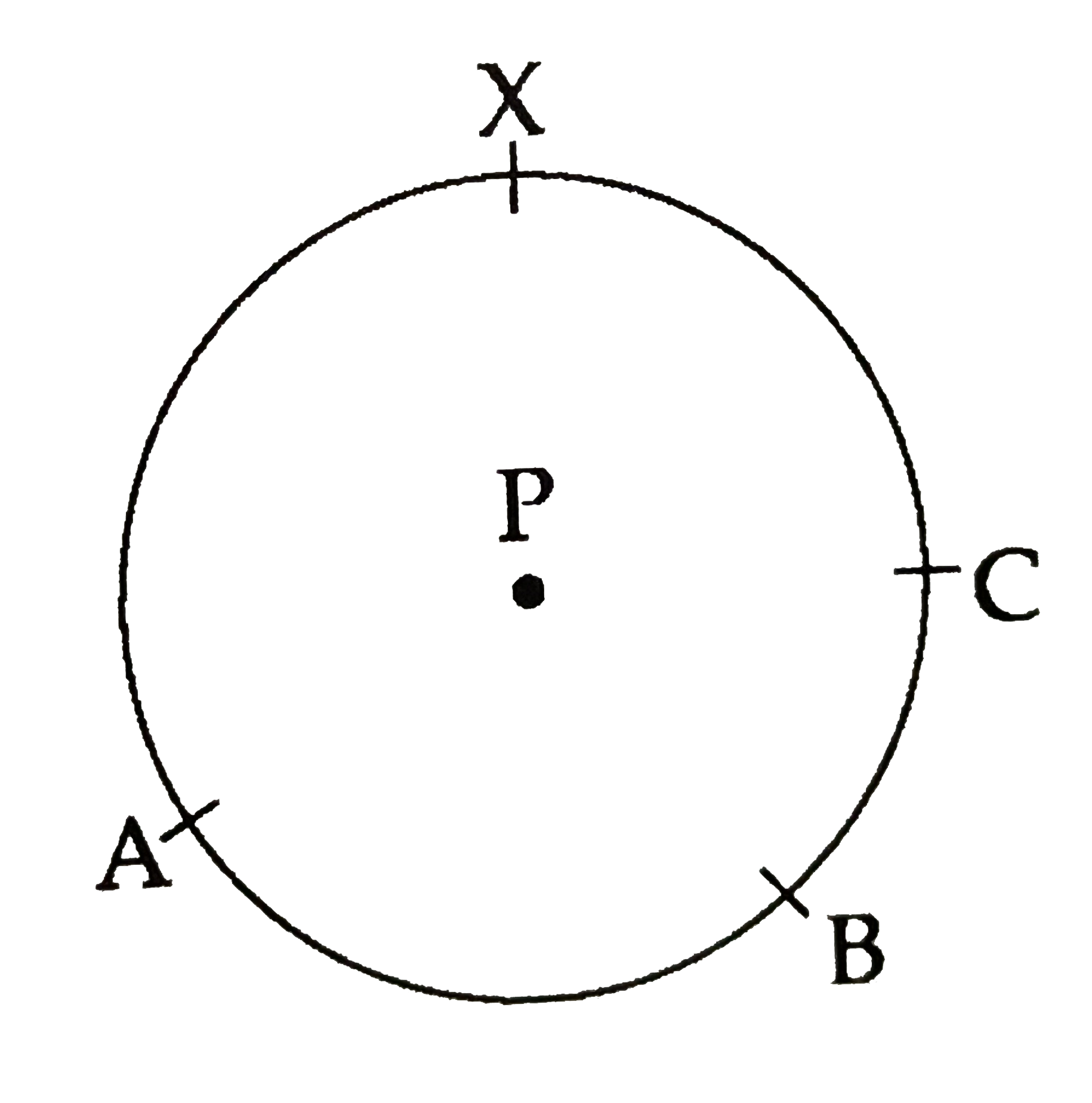
View SolutionA circle with centre P. arc AB = arc BC and arc AXC = 2 arc AB . Find measure of arc AB, arc BC and arc AXC. Prove that chord AB≅ chord BC .
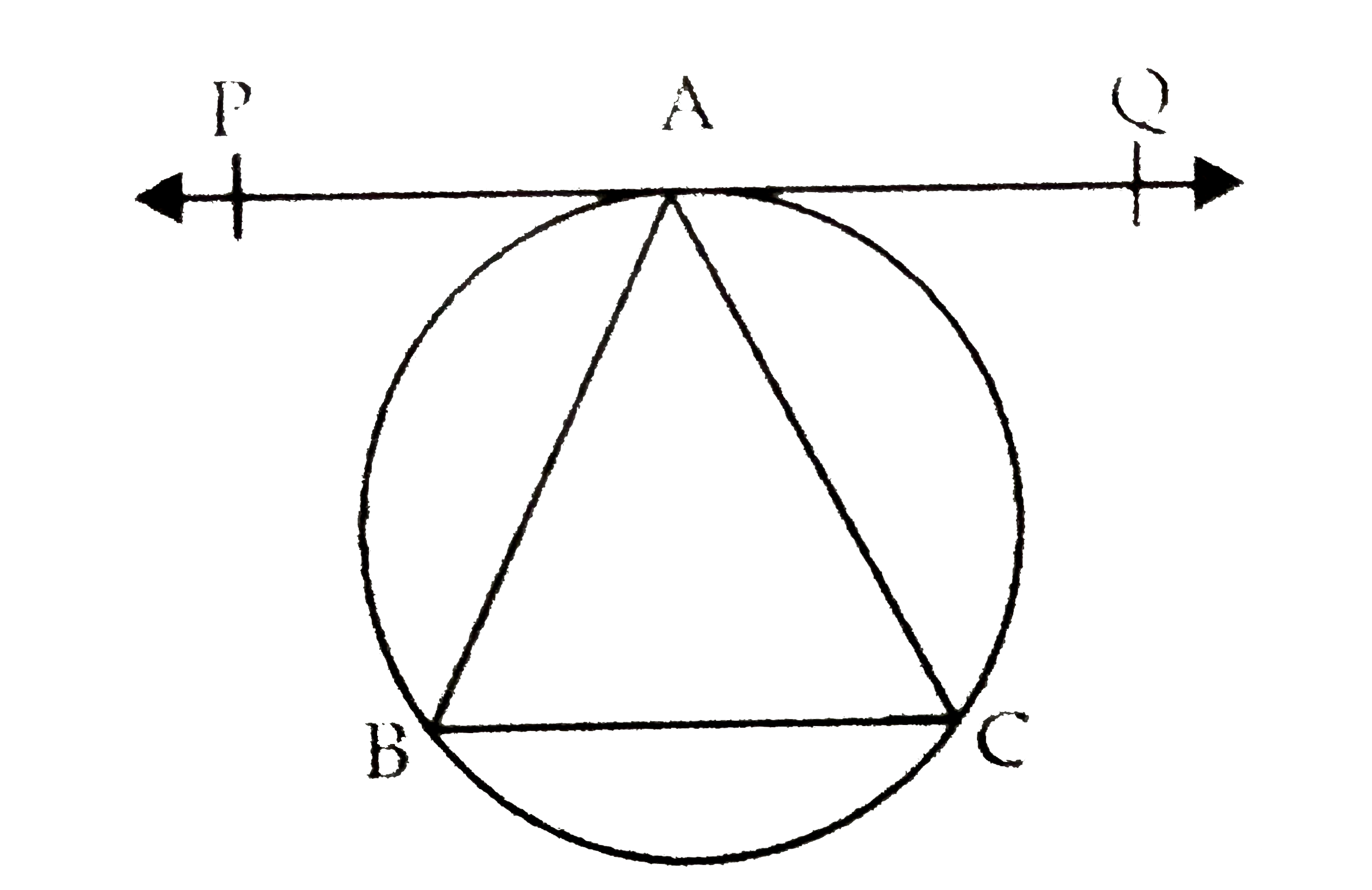
View SolutionLine PQ is a tangent to the circle at point AB ≅ arc AC. Complete the following activity to prove ΔABC as isosceles triangle.
View SolutionFrom the point (4, 6) a pair of tangent lines are drawn to the parabola, y2=8x. The area of the triangle formed by these pair of tangent lines & the chord of contact of the point (4, 6) is
View SolutionFrom a point A(3,2) , tangents are drawn to the circle x2+y2−2x+4y−4=0 . If BC is the chord of contact of tangents , show that the line joining the midpoints of AB and AC is 4x+8y-17=0
View Solution. Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
View Solution

