A wave is propagating along the length of a string taken as positive x-axis. The wave equation is given by
y=Ae−(tT−xλ)2
where A=5mm, T=1.0 s and λ=8.0cm
(a) Find the velocity of the wave.
(b) find the function f(t) represent the displacement of particle at x=0.
(c ) Plot the function g(x) representing the shape of the string at t=0
(d) Plot the function g(x) of the string at t=0 and t=5 s
The wave equation may be written as
y=y0e−tT2{t−xλ/T}2
Putting x = 0 in the given equation
f(t)=y0e−(t/T)2
Topper's Solved these Questions
- SOUND WAVESBook:MOTIONChapter:SOUND WAVESExercise:Questions for practice
Explore 12 Videos
- SOUND WAVESBook:MOTIONChapter:SOUND WAVESExercise:Exercise - 1
Explore 82 Videos
- SOUND WAVESBook:MOTIONChapter:SOUND WAVESExercise:EXERCISE - 4 ( LEVEL II)
Explore 24 Videos
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -4 (Leve-II) [ JEE 2011]
Explore 11 Videos
- SURFACE TENSIONBook:MOTIONChapter:SURFACE TENSIONExercise:Exercise - 3 | Section - B Previous Year Problems | AIEEE
Explore 12 Videos
Similar Questions
A person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360ms−1.
View SolutionThe ratio (V) of velocities of sound in dry air and humid air is -
View SolutionIn a resonance column method, resonance occurs at two successive level of l1=30.7cm and l2=63.2cm using a tuning fork of f=512Hz. What is the maximum error in measuring speed of sound using relations v=fλ&λ=2(l2−l1)
View SolutionWhen a particle is mass m moves on the x− axis in a potential of the from V(x)=kx2, it performs simple harmonic motion. The corresponding thime periond is proportional to √mk, as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides x=0 in a way different from kx2 and its total energy is such that the particel does not escape to infinity. consider a particle of mass m moving onthe x−axis . Its potential energy is V(x)=ω(α>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0 (see figure)
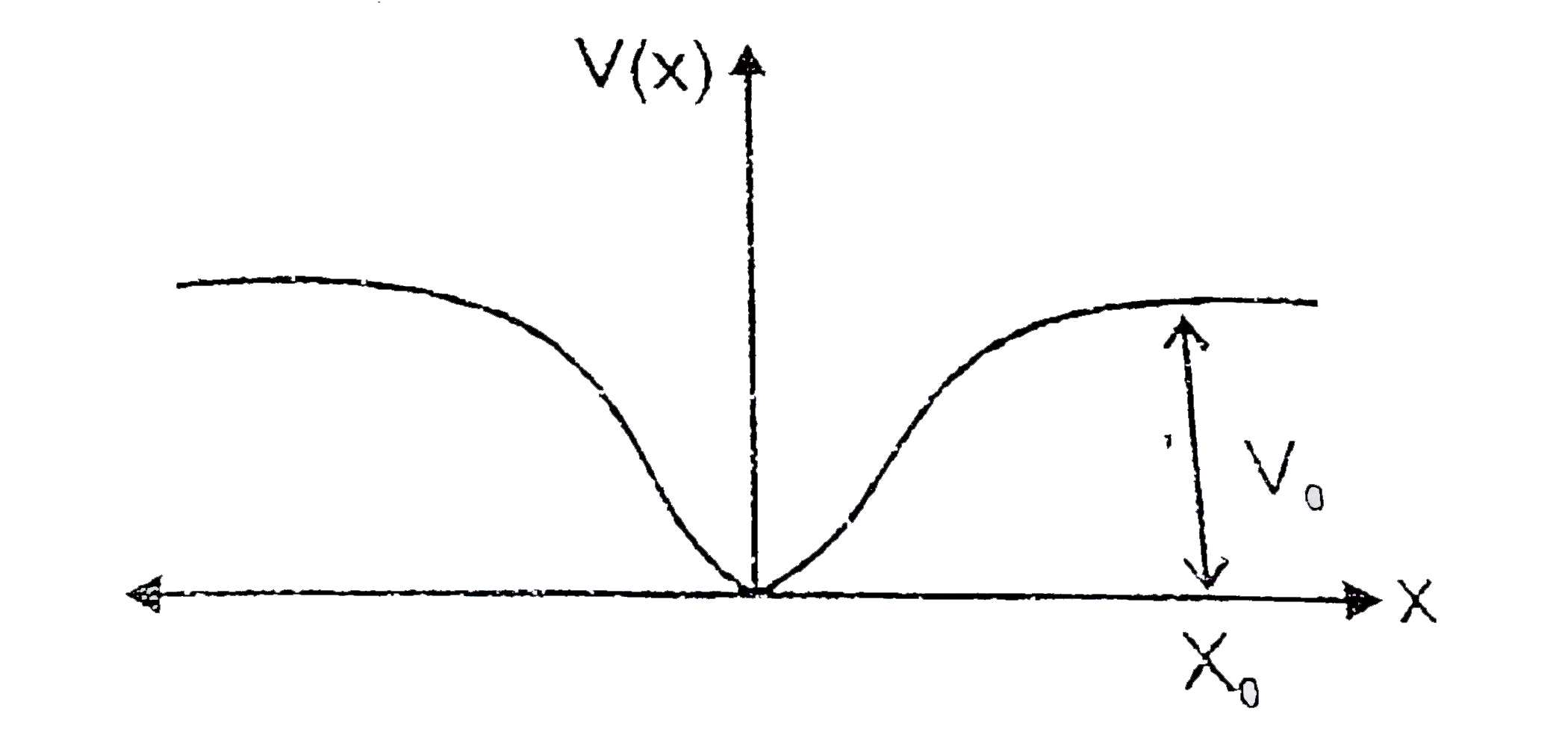
If the total energy of the particle is E, it will perform is periodic motion why if :
View SolutionA 20 cm long capillary tube is dipped in water. The water rises up to 8 cm. If the entire arrangement is put in a freely falling elevator, the length of water column in the capillary tube will be
View SolutionA wave is propgting of a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)^2
where y0=4mm,T=1.0sandλ=4cm. d. Find the velocity of the particle t x=0. c. Find the function g(x) giving the shape of the string t t=0. d. Plot the shape g(x) of the string at t=0. e. Plot of the shape of the string at t=5s.
View SolutionA wave pulse on a horizontal string is represented by the function
y(x,t)=5.01.0+(x−2t)2 (CGS units)
plot this function at t=0,2.5 and 5.0s.
View SolutionThe equation of a wave travelling on a string stretched along the X-axis is given by
y=Ae(−xa+tT)2
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling?
(d) Where is the maximum of the pulse located at t=T and at t=2T?
View SolutionIf at t=0, a travelling wave pulse in a string is described by the function,
y=10(x2+2)
Hence, xandy are in meter and t in second. What will be the wave function representing the pulse at time t, if the pulse is propagating along positive x-axix with speed 2m/s?
View SolutionA pulse moving to the right along the x-axis is represented by the wave function
where x and y are measured in cedntimetres and t is measured in seconds. Find expression for the wave function at t=0,t=1.0s,andt=2.0s and plote the shape of pulse at these lines.
View SolutionA wave is propagating along the length of a string taken as positive x-axis. The wave equation is given by y=Ae^((-t/t-x/A)^(2)) where A=5mm, T=1.0 s and lambda=8.0 cm (a) Find the velocity of the wave. (b) find the function f(t) represent the displacement of particle at x=0. (c ) Plot the function g(x) representing the shape of the string at t=0 (d) Plot the function g(x) of the string at t=0 and t=5 s
View SolutionA wave pulse moving along the x axis is represented by the wave funcation
y(x,t)=2(x−3t)2+1
where x and y are measured in cm and t is in seconds.
(i) in which direction is the wave moving ?
(ii) Find speed of the wave.
(iii) Plot the waveform at t=0,t=2s.
View Solutionएक लंबी तनी हुई डोरी पर एक तरंग धनात्मक -दिशा में चल रही है । इसका समीकरण है
y=y0e−(xλ−tT)2
जहाँ y0=4mm, T=1.0s तथा λ=4cm है । (a) तरंग की चाल बताएँ| (b) समय t के साथ x=0 के कण के विस्थपन के लिए फलन f(t) बताएँ । (c ) t=0 पर डोरी के विभिन्न कणों के विस्थापन के लिए फलन g(x) बताएँ । (d) t=0 पर डोरी की सकल बताने के लिए ग्राफ खींचे तथा (e) t = 5 s पर डोरी की शक्ल बताने के लिए ग्राफ खींचें ।
View SolutionA wave is propagating on a long stretched string along its length taken as positive x-axis the wave equation is given by y = y_(0) e^(-((t)/(T)-(x)/(lambda))^(2)),"where" y_(0) = 2 m m T = 1 . 0 sec and lambda = 6 cm find . Plot the shape of the string at t = 6 sec.
View SolutionA wave is propagating on a long stretched string along its length taken as positive x-axis the wave equation is given by
y=y0e−(tT−xλ)2,wherey0=2mm
T = 1 . 0 sec and λ=6cm find .
Plot the shape of the string at t = 6 sec.
View SolutionAt t = 0 a travelling wave pulse on a string is described by the function y=10x2+2 , here x and y are in meter and t in second. What will be the wave function representing the pulse at time t, if the pulse is propagating along the positive x-axis with speed 2m/s ?
View Solution
