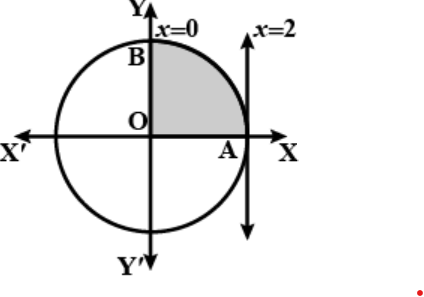
Area lying in the first quadrant and bounded by the circle x2+y2=4 and the lines x=0andx=2 is
(A) π (B) π2 (C) π3 (D) π4
The correct Answer is:A
The area bounded by the circle and the lines, x=0 and x=2, in the first quadrant is represented as shaded region in the plot.
Area of △OAB=∫20ydx
=∫20√4−x2dx
=[x2√4−x2+42sin−1(x2)]20
=2(π2) = π sq. units
Similar Questions
Area lying in the first quadrant and bounded by the circle x2+y2=4 and the lines x=0 and x=2 is:
View SolutionFind the area of the circle x2+y2=4 bounded by the lines x = 0 and x = 2 which is lying in the first quadrant.
View SolutionArea lying in the first quadrant and bounded by the circle x2+y2=4 and the lines x = 0 and x = 2 is
View SolutionArea lying in the first quadrant and bounded by the circle x2+y2=4 and the lines x=0 and x=2 is :
View SolutionArea lying in the first quadrant and bounded by the circle x2+y2=4 and the line x=0 and x=2 is
View SolutionArea lying in the first quadrant and bounded by the circle x2+y2=4
the line x=√3y and x-axis , is
(a) π2
(b) π4
(c) π3
(d) π
View SolutionThe area bounded by y=sin2x,x=π2andx=π is a)π2 b)π4 c)π8 d)π16
View SolutionArea lying in the first quadrant and bounded by the circle x2+y2=4and the lines x=0andx=2is(A) π (B) π2 (C) π3 (D) π4
View Solution
